题目内容
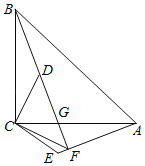
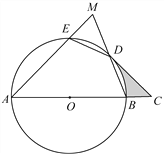
【题目】如图,AB是⊙O的直径,![]() ,连接ED,BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
,连接ED,BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA=CD=2![]() ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE=DM.
【答案】(1)4-π(2)证明见解析
【解析】
试题(1)连接OD,由已知条件可证出三角形ODC是等腰直角三角形,OD的长度知道,∠DOB的度数是45度,这样,阴影的面积就等于等腰直角三角形ODC的面积减去扇形ODB的面积;
(2)连接AD,由已知条件可证出AD垂直平分BM,从而得到DM=DB,又因为弧DE=弧DB,DE=DB,所以DE就等于DM.
试题解析:(1)连接OD,
∵CD是⊙O切线,
∴OD⊥CD∵OA=CD =![]() ,
,
OA=OD∴OD=CD=![]()
∴△OCD 为等腰直角三角形∠DOC=∠C=45°
S阴影=S△OCD-S扇OBD=![]() ×
×![]() ×
×![]() -
-![]() =4-π;
=4-π;
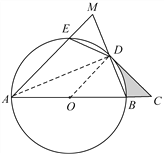
(2)连接AD.
∵AB是⊙O直径
∴∠ADB=∠ADM= 90°
又∵弧ED=弧BD
∴ED=BD ∠MAD=∠BAD
∴△AMD≌△ABD
∴DM=BD
∴DE=DM.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数。
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?