题目内容
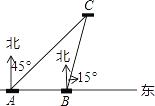
【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.
【答案】20![]()
【解析】
首先过点B作BD⊥AC于点D,进而利用BD=ABsin∠BAD,BC=![]() 求出即可
求出即可
过点B作BD⊥AC于点D,
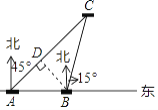
由题意可知:∠BAC=45°,∠ABC=90°+15°=105°,
则∠ACB=180°﹣∠BAC﹣∠ABC=30°,
在Rt△ABD中,BD=ABsin∠BAD=20×![]() =10
=10![]() ,
,
在Rt△BCD中,BC= ![]() =20
=20![]() .
.
答:此时船C与船B的距离是20![]() 海里.
海里.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是( )
A. 抛物线的开口向下
B. 当x>﹣![]() 时,y随x的增大而增大
时,y随x的增大而增大
C. 二次函数的最小值是﹣2
D. 抛物线的对称轴是x=1