题目内容
【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。
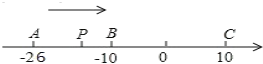
(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
【答案】(1)t;36-t;(2)①24;②30.
【解析】
(1)利用数轴上两点的距离公式求出AC的长度,根据路程=速度×时间,用t表示出AP,
再利用PC=AC-AP即可;
(2)①先利用数轴上两点的距离公式求出BC的长度,再利用时间=路程÷速度算出P从B运动到C的时间,算出Q的运动路程,最后减去AC即可;
②先利用AB的长度算出Q比P晚出发的时间,再利用P和Q运动总路程等于两个AC的长度列方程即可.
解:(1)由数轴可知:AC=10-(﹣26)=36个单位长度
∵动点P从A出发,以每秒1个单位的速度向终点C移动
PA=t,PC=36-t;
(2)①由数轴可知:BC=10-(﹣10)=20个单位长度,
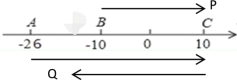
∴P从B运动到C的时间为:20÷1=20s
∵当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动
∴当P从B运动到C时,Q的运动时间也是20s
∴Q的运动路程为:20×3=60个单位长度,
∵此时P在C处
∴QP=QC=60-AC=60-36=24.
②由数轴可知:AB=(﹣10)-(﹣26)=16个单位长度,
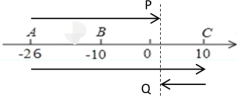
∵当点P运动到B点时,点Q从A点出发,
∴Q比P晚出发了:16÷1=16s
故Q的运动时间为(t-16)s,
由图可知:P和Q运动总路程等于两个AC的长度
∴t+3(t-16)=2×36
解得:t=30
答:当t等于30时,P、Q两点恰好在途中相遇