题目内容
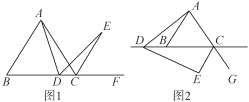
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
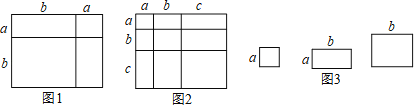
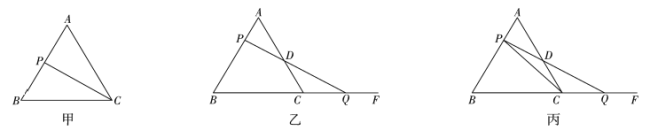
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由BC⊥AF可得∠A+∠B=90°,又因为∠A+∠1=90°,根据同角的余角相等可证∠B=∠1,从而AB∥DE.
(2)分①点P在A,D之间时,②当点P在C,D之间时,③点P在C,F之间时三种情况,分别过P作PG∥AB,根据平行线的性质求解即可.
(1)如图1,∵BC⊥AF于点C,
∴∠A+∠B=90°,
又∵∠A+∠1=90°,
∴∠B=∠1,
∴AB∥DE.
(2)如图2,当点P在A,D之间时,过P作PG∥AB,
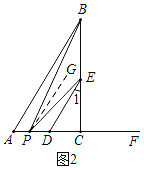
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG+∠EPG=∠ABP+∠DEP;
如图所示,当点P在C,D之间时,过P作PG∥AB,
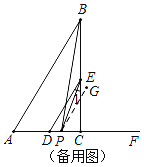
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG﹣∠EPG=∠ABP﹣∠DEP;
如图所示,当点P在C,F之间时,过P作PG∥AB,

∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠EPG﹣∠BPG=∠DEP﹣∠ABP.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目