Question

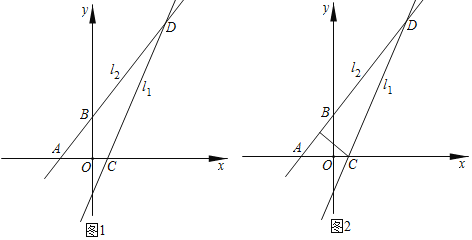
【题目】如图1，在平面直角坐标系中将向下平移3个单位长度得到直线，直线与x轴交于点C；直线：与x轴、y轴交于A、B两点，且与直线交于点D．

填空：点A的坐标为______，点B的坐标为______；

直线的表达式为______；

在直线上是否存在点E，使？若存在，则求出点E的坐标；若不存在，请说明理由．

如图2，点P为线段AD上一点不含端点，连接CP，一动点H从C出发，沿线段CP以每秒1个单位的速度运动到点P，再沿线段PD以每秒个单位的速度运动到点D后停止，求点H在整个运动过程中所用时间最少时点P的坐标．

Answer 1

【答案】（1） ；（2）；（3）点E的坐标为；（4）点H在整个运动过程中所用最少时间为6秒，此时点P的坐标．

【解析】

直线：，令，则，令，则，即可求解；

根据平移的性质即可求解；

，即：，即可求解；

点H在整个运动过程中所用时间，当C、P、H在一条直线上时，最小，即可求解．

直线：，令，则，令，则，

故答案为、；

向下平移3个单位长度得到直线，则直线的表达式为：，

故：答案为：；

，

，

将代入的表达式得：，解得：，

则点E的坐标为；

过点P、C分别作y轴的平行线，分别交过点D作x轴平行线于点H、，交BD于点，

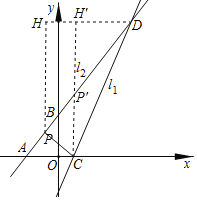
直线：，则，，

点H在整个运动过程中所用时间，

当C、P、H在一条直线上时，最小，即为，点P坐标，

故：点H在整个运动过程中所用最少时间为6秒，此时点P的坐标．