��Ŀ����
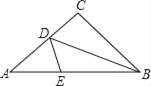
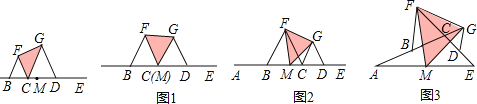
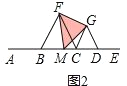
����Ŀ����ͼ1��ͼ3�У���B���߶�AC���е㣬��D��CE���е㣬��BCF����CDG���ǵȱ������Σ���MΪAE���е㣬����FG��
��1����ͼ1������E��AC���ӳ����ϣ���M���C�غϣ�����FMG�������������ȱ������Σ���������������������
��2����ͼ1�е�CE���̣��õ�ͼ2����֤����FMGΪ�ȱ������Σ�
��3����ͼ2�е�CE�Ƶ�E˳ʱ����תһ����ǣ��õ�ͼ3����֤����FMGΪ�ȱ������Σ�
���𰸡���1���ǣ���2��֤������������3��֤��������.
��������
(1)��ͼ1,��֤FM=BM=MD=MG, ��FMG=60��,���ɵõ���FMG�ǵȱ�������;(2)��ͼ2,��֤BD=BC+CD=AM,�Ӷ��ɵ�MD=AB.����BCF����CDG���ǵȱ�������,�ɵ�BF=BC,CD=GD, ��FBC=60��, ��GDC=60��,�Ӷ���֤��MD=BF,BM=GD,�����ɵõ���FBM�ա�MDG,����MF=GM, ��BFM=��DMG,�Ӷ���֤����FMG=60��,���ɵõ���FMGΪ�ȱ�������;(3)��ͼ3,����BM��DM,������������λ�߶����ɵ�BM��CE,BM=![]() CE=CD,DM��AC,DM=
CE=CD,DM��AC,DM=![]() AC=BC.�ٸ�����BCF����CDG���ǵȱ�������,�ɵ�BF=BC,CD=GD, ��FBC=60��, ��GDC=60��,�Ӷ��õ�BF=BC=DM,BM=CD=GD, ��FBC=��GDC.��BM��CE,DM��AC,�ɵ��ı���BCDM��ƽ���ı���,�Ӷ��õ���BMD=��DCB=120��, ��CDM=��MBC=60��,���ɵõ���FBM=��GDM=120��,���ɵõ���FBM�ա�MDG,����MF=GM, ��FMB=��MGD,�Ӷ��ɵá�FMG=��BMD-��FMB-GMD=��BML,���ɵõ���FMGΪ�ȱ�������.
AC=BC.�ٸ�����BCF����CDG���ǵȱ�������,�ɵ�BF=BC,CD=GD, ��FBC=60��, ��GDC=60��,�Ӷ��õ�BF=BC=DM,BM=CD=GD, ��FBC=��GDC.��BM��CE,DM��AC,�ɵ��ı���BCDM��ƽ���ı���,�Ӷ��õ���BMD=��DCB=120��, ��CDM=��MBC=60��,���ɵõ���FBM=��GDM=120��,���ɵõ���FBM�ա�MDG,����MF=GM, ��FMB=��MGD,�Ӷ��ɵá�FMG=��BMD-��FMB-GMD=��BML,���ɵõ���FMGΪ�ȱ�������.
��1����ͼ1��

�ߵ�B���߶�AC���е㣬��D��CE���е㣬��MΪAE���е㣬��M���C�غϣ�
��AB=BM=AM=ME=MD=DE��
�ߡ�BCF����CDG���ǵȱ������Σ���M���C�غϣ�
��FM=BM��MD=GM��
��FM=GM��
�ߡ�FMG=180�㩁60�㩁60��=60�㣬
���FMG�ǵȱ������Σ�
�ʴ�Ϊ���ǣ�
��2����ͼ2��
�ߵ�B���߶�AC���е㣬��D��CE���е㣬��MΪAE���е㣬
��AB=BC=AC��CD=DE=CE��AM=ME=AE��
��BD=BC+CD=AC+CE=AE=AM����BM+MD=BM+AB��
��MD=AB��
�ߡ�BCF����CDG���ǵȱ������Σ�
��BF=BC��CD=GD����FBC=60�㣬��GDC=60�㣬
��MD=AB=BC=BF��BM=BC��MC=MD��MC=CD=GD��
����FBM����MDG��
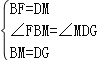 ��
��
���FBM�ա�MDG��
��MF=GM����BFM=��DMG��
�ߡ�BFM+��FMB+��FBM=180�㣬��DMG+��FMB+��FMG=180�㣬
���FMG=��FBM=60�㣬
���FMGΪ�ȱ������Σ�
��3����ͼ3������BM��DM��
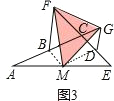
�ߵ�B���߶�AC���е㣬��D��CE���е㣬��MΪAE���е㣬
��BM��CE��BM=CE=CD��DM��AC��DM=AC=BC��
�ߡ�BCF����CDG���ǵȱ������Σ�
��BF=BC��CD=GD����FBC=60�㣬��GDC=60�㣬
��BF=BC=DM��BM=CD=GD����FBC=��GDC��
��BM��CE��DM��AC��
���ı���BCDM��ƽ���ı��Σ�
���BMD=��DCB=120�㣬��CDM=��MBC=60�㣬
���FBM=��GDM=120�㣮
����FBM����MDG��
 ��
��
���FBM�ա�MDG��
��MF=GM����FMB=��MGD��
���FMG=��BMD����FMB����GMD=��BMD����MGD����GMD
=120�㩁��180�㩁120�㣩=60�㣬
���FMGΪ�ȱ������Σ�

����Ŀ��ѧУ���ۺ�ʵ�������ѧϰС�����ѧУУ�칤����������������ڹ���ʦ����ָ���Ͱ����£��ۺ�ʵ�������ѧϰС��һ�ܼƻ�����700������ƽ��ÿ������100�������ڸ���ԭ��ʵ��ÿ������������ƻ�������г��룬�±���ij�ܵ��������������Ϊ��������Ϊ������
���� | һ | �� | �� | �� | �� | �� | �� |
���� |
|
|
|
|
|
|
|
��1�����ݼ�¼��֪ǰ���칲���� ����
��2����������һ��Ȳ������ٵ�һ������� ����
��3����У�칤��ʵ��ÿ�ܼƼ������ƣ�����һ�����������ۺ�ʵ�������ѧϰС��![]() Ԫ��������������ÿ���ٽ�
Ԫ��������������ÿ���ٽ�![]() Ԫ����ô��У���ۺ�ʵ�������ѧϰС����һ�ܵõ��Ľ����ܶ��Ƕ���Ԫ?
Ԫ����ô��У���ۺ�ʵ�������ѧϰС����һ�ܵõ��Ľ����ܶ��Ƕ���Ԫ?