题目内容
【题目】已知函数y=ax2与直线y=2x﹣3的图象交于点A（1，b）．
（1）求a，b的值；
（2）求两函数图象另一交点B的坐标．
【答案】（1）a=﹣1，b=﹣1（2）（﹣3，﹣9）
【解析】（1）要求出b的值，只需要将点A的坐标代入一次函数关系式，如此即可求出b的值；由b的值即可求出点A的坐标，然后代入y=ax2中，从而即可求出a的值；
（2只需要将两个函数关系式联立，解方程组即可得出交点B坐标.
（1）解：函数y=ax2与直线y=2x﹣3的图象交于点A（1，b）， ∴A（1，b）代入y=2x﹣3 得 b=2×1﹣3=﹣1，
∴A（1，﹣1），
∴﹣1=a12 ， 解得a=﹣1，
∴a=﹣1，b=﹣1
（2）解：依题意得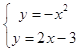 
， 解得 
， 
．
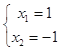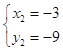故两函数图象另一交点B的坐标为（﹣3，﹣9）
练习册系列答案
小学期末标准试卷系列答案
相关题目
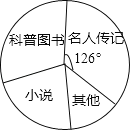
【题目】2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动，200多所学校的师生踊跃参与，向新疆疏勒县中小学共捐赠爱心图书28.5万余本．某学校学生社团对本校九年级学生所捐图书进行统计，根据收集的数据绘制了下面不完整的统计图表．请你根据统计图表中所提供的信息解答下列问题：
图书种类 | 频数（本） | 频率 |
名人传记 | 175 | a |
科普图书 | b | 0.30 |
小说 | 110 | c |
其他 | 65 | d |
（1）求该校九年级共捐书多少本；
（2）统计表中的a= ，b= ，c= ，d= ；
（3）若该校共捐书1500本，请估计“科普图书”和“小说”一共多少本；
（4）该社团3名成员各捐书1本，分别是1本“名人传记”，1本“科普图书”，1本“小说”，要从这3人中任选2人为受赠者写一份自己所捐图书的简介，请用列表法或树状图求选出的2人恰好1人捐“名人传记”，1人捐“科普图书”的概率．
