题目内容
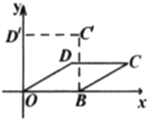
【题目】如图，在
中，
，将绕点
逆时针旋转
，得到
，其中点
的对应点分别为点
连接
在旋转过程中，若
，则
的长为_________．
【答案】
【解析】
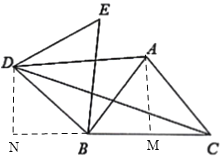
如图，过点A作AM⊥BC于M，过点D作DN⊥BC，交CB延长线于N，根据旋转的性质可得∠EBC=∠DBA，BD=AB，可得BD=AC，由
可得∠DBA=∠BAC，即可证明BD//AC，可证明四边形DBCA是平行四边形，可得AM=DN，根据等腰三角形“三线合一”的性质可得BM=
BC，利用勾股定理可求出AM的长，可得DN的长，利用勾股定理可求出BN的长，进而可得CN的长，利用勾股定理求出CD的长即可．
如图，过点A作AM⊥BC于M，过点D作DN⊥BC，交CB延长线于N，
∵AB=AC=5，BC=6，AM⊥BC，
∴BM=BC=3，
∴AM=
=4，
∵将
绕点
逆时针旋转
，得到
，
∴∠EBC=∠DBA，BD=AB=AC=5，
∵，
∴∠DBA=∠BAC，
∴BD//AC，
∴四边形DBCA是平行四边形，
∴DN=AM=4，
∴BN=
=3，
∴CN=BC+BN=9，
∴CD=
=，
故答案为：
练习册系列答案
相关题目
