题目内容
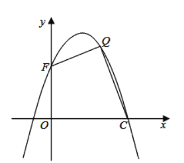
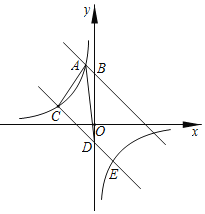
【题目】如图,在平面直角坐标系中,直线AB与y轴交于点![]() ,与反比例函数
,与反比例函数![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() .
.
(1)求直线AB的解析式;
(2)将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E,与y轴交于点D,求![]() 的面积;
的面积;
(3)设直线CD的解析式为![]() ,根据图象直接写出不等式
,根据图象直接写出不等式![]() 的解集.
的解集.
【答案】(1))![]() ;(2)
;(2)![]() 的面积为18;(3)
的面积为18;(3)![]() 或
或![]() .
.
【解析】
(1)将点A(-1,a)代入反比例函数![]() 求出a的值,确定出A的坐标,再根据待定系数法确定出一次函数的解析式;
求出a的值,确定出A的坐标,再根据待定系数法确定出一次函数的解析式;
(2)根据直线的平移规律得出直线CD的解析式为y=-x-2,从而求得D的坐标,联立方程求得交点C、E的坐标,根据三角形面积公式求得△CDB的面积,然后由同底等高的两三角形面积相等可得△ACD与△CDB面积相等;
(3)根据图象即可求得.
(1))∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() ,
,
∵点![]() ,
,
∴设直线AB的解析式为![]() ,
,
∵直线AB过点![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)∵将直线AB向下平移9个单位后得到直线CD的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
联立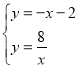 ,解得
,解得![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
连接AC,则![]() 的面积
的面积![]() ,
,
由平行线间的距离处处相等可得![]() 与
与![]() 面积相等,
面积相等,
∴![]() 的面积为18.
的面积为18.
(3)∵![]() ,
,![]() ,
,
∴不等式![]() 的解集是:
的解集是:![]() 或
或![]() .
.

练习册系列答案
相关题目