题目内容
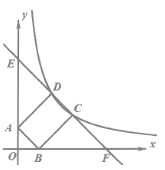
【题目】如图,抛物线y=﹣x2+bx+c(a≠0)与x轴、y轴分别交于点A(3,0)、B(0,3)两点.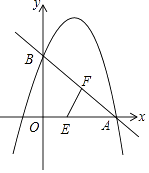
(1)试求抛物线的解析式和直线AB的解析式;
(2)动点E从O点沿OA方向以1个单位/秒的速度向终点A匀速运动,同时动点F沿AB方向以 ![]() 个单位/秒的速度向终点B匀速运动,E、F任意一点到达终点时另一个点停止运动,连接EF,设运动时间为t,当t为何值时△AEF为直角三角形?
个单位/秒的速度向终点B匀速运动,E、F任意一点到达终点时另一个点停止运动,连接EF,设运动时间为t,当t为何值时△AEF为直角三角形?
(3)抛物线位于第一象限的图象上是否存在一点P,使△PAB面积最大?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=﹣x2+bx+c(a≠0)经过A(3,0),B(0,3),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3,
设直线y=kx+n,
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线AB的解析式为y=x+3
(2)
解:由题意可知OE=t,则AF= ![]() t,AE=3﹣t,
t,AE=3﹣t,
∵△AEF为直角三角形,
∴有∠AEF=90°和∠AFE=90°两种情况,
①当∠AEF=90°时,则有△AOB∽△AEF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=
,解得t= ![]() ;
;
②当∠AFE=90°时,则有△AOB∽△AFE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=1;
,解得t=1;
综上可知当t为 ![]() 或1时△AEF为直角三角形
或1时△AEF为直角三角形
(3)
解:如图,过P作PC∥y,AB于点C,交x轴于点D,
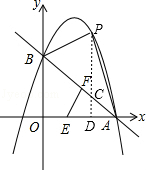
设P(x,﹣x2+2x+3)(0<x<3),则C(x,﹣x+3),
∵P为抛物线在第一象限内的点,
∴PC=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x,
∴S△PAB=S△PBC+S△PAC= ![]() PCOD+
PCOD+ ![]() PCAD=
PCAD= ![]() PCOA=
PCOA= ![]() PC=
PC= ![]() (﹣x2+3x)=﹣
(﹣x2+3x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当x= ![]() 时,S△PAB有最大值
时,S△PAB有最大值 ![]() ,此时P点坐标为(
,此时P点坐标为( ![]() ,
, ![]() ),
),
综上可知存在满足条件的点P,其坐标为( ![]() ,
, ![]() )
)
【解析】(1)根据A、B两点的坐标,利用待定系数法可求得抛物线和直线AB的解析式;(2)骼t可表示出OE、AF、AE的长,分∠AEF=90°和∠AFE=90°两种情况,可分别证明△AOB∽△AEF和△AOB∽△AFE,利用相似三角形的性质可得到关于t的方程,可求得t的值;(3)过P作PC∥y,AB于点C,交x轴于点D,可设出P点坐标,用P点坐标可表示也PC的长,从而可表示出△PAB的面积,根据二次函数的性质可求得其取得最大值时P点的坐标.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小),还要掌握相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形)的相关知识才是答题的关键.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案