题目内容
【题目】如图,在平面直角坐标系中,直线EF交x,y轴子点F,E,交反比例函数![]() (x>0)图象于点C,D,OE=OF=
(x>0)图象于点C,D,OE=OF=![]() ,以CD为边作矩形ABCD,顶点A与B恰好落在y轴与x轴上.
,以CD为边作矩形ABCD,顶点A与B恰好落在y轴与x轴上.
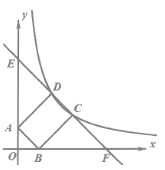
(1)若矩形ABCD是正方形,求CD的长;
(2)若AD:DC=2:1,求k的值.
【答案】(1)![]() ;(2)k=12
;(2)k=12
【解析】(1)根据等腰三角形的性质以及勾股定理可得EF的长,继而根据正方形的性质即可得DE=DC=CF,从而即可求得CD的长;
(2)由四边形ABCD是矩形,可得AD=BC,根据(1)得:AD=DE,BC=FC,且 2CD=AD,从而可得 2CD=DE=CF,根据DE+CD+FC=EF,继而可求得DE的长,作 DG⊥AE,垂足为点 G,在等腰直角三角形 ADE 中,求得DG=EG = 2![]() ,继而求得OG长,从而可得点D( 2
,继而求得OG长,从而可得点D( 2![]() , 3
, 3![]() ) ,即可求得k.
) ,即可求得k.
(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,
∠ADC=∠BCD=90°,
∴∠ADE=∠BCF=90°,
∵OE=OF= 5![]() ,
,
又∵∠EOF=90°,
∴∠OEF=∠OFE=45°,FE=10,
∴CD=DE=AD=CB=CF=![]() ;
;
(2)∵四边形ABCD是矩形,
∴AD=BC,
∵由(1)得:AD=DE,BC=FC,且 2CD=AD,
∴2CD=DE=CF,
∵DE+CD+FC=EF,
∴DE= ![]() EF =4,
EF =4,
作 DG⊥AE,垂足为点 G,
由(1)得在等腰直角三角形 ADE 中,DG=EG=![]() DE = 2
DE = 2![]() ,
,
∴OG=OE-EG= 5![]() - 2
- 2![]() = 3
= 3![]() ,
,
∴D( 2![]() , 3
, 3![]() ) ,
) ,
得:k=12.


练习册系列答案
相关题目