题目内容
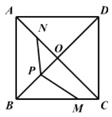
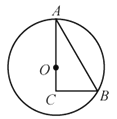
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B.
(1)求⊙O的半径;
(2)点P为![]() 中点,作PQ⊥AC,垂足为Q,求OQ的长;
中点,作PQ⊥AC,垂足为Q,求OQ的长;
(3)在(2)的条件下,连接PC,求tan∠PCA的值.
【答案】(1)⊙O的半径为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)若连接OB,则△BCO是一个含30°角的直角三角形,△AOB是底角为30°的等腰三角形,可得∠OBC=30°,再根据特殊角的三角函数值求得OB;
(2) 连接OP,设AB与QP交于点M,根据题中条件证得∠QPO=∠A=30°,再根据特殊角的三角函数值求得OQ;
(3)可在Rt△PCQ中解决,分别计算出两条直角边,即可求出tan∠PCA的值.
(1)连接OB,如图
∵OA=OB,
∴∠ABO=∠A=30°,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∴∠OBC=30°,
在Rt△OBC中,![]() ,
,
即![]() ,
,
解得![]() ,
,
即⊙O的半径为![]() ;
;
(2)连接OP,设AB与QP交于点M,
∵点P为![]() 的中点,
的中点,
∴OP⊥AB,
∴∠QPO+∠PMB=90°,
∵PQ⊥AC,
∴∠A+∠AMQ=90°,
又∵∠AMQ=∠PMB,
∴∠QPO=∠A=30°,
在Rt△OPQ中,![]() ,
,
即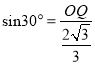 ,
,
∴![]()
(3)在Rt△OBC中,
∵![]() ,∠OBC=30°,∠ACB=90°
,∠OBC=30°,∠ACB=90°
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目