题目内容
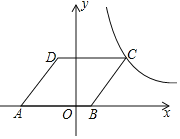
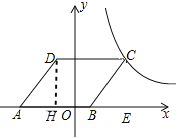
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
【答案】16
【解析】
过点D作DH⊥x轴,垂足为H,由已知则可得H(-1,0),DH=4,根据点A(-4,0),可得AH=3,要卖勾股定理可求得AD长,再根据菱形的性质可得DC=AD=5,DC//AB,根据平移的性质可得C(4,4),再利用待定系数法即可求得答案.
过点D作DH⊥x轴,垂足为H,则∠AHD=90°,
又∵D(-1,4),
∴H(-1,0),DH=4,
∵A(-4,0),
∴AH=3,
∴AD=![]() =5,
=5,
∵四边形ABCD是菱形,
∴DC=AD=5,DC//AB,
∴C(4,4),
∵反比例函数![]() 的图象恰好经过点C,
的图象恰好经过点C,
∴4=![]() ,
,
∴k=16,
故答案为16.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某商店出售一款商品,经市场调查反映,该商品的日销售量y(件)与销售单价x(元)之间满足一次函数关系,关于该商品的销售单价,日销售量,日销售利润的部分对应数据如表:[注:日销售利润=日销售量×(销售单价﹣成本单价)
销售单价x(元) | 75 | 78 | 82 |
日销售量y(件) | 150 | 120 | 80 |
日销售利润w(元) | 5250 | a | 3360 |
(1)根据以上信息,填空:该产品的成本单价是 元,表中a的值是 ,y关于x的函数关系式是 ;
(2)求该商品日销售利润的最大值.
(3)由于某种原因,该商品进价降低了m元/件(m>0),该商店在今后的销售中,商店规定该商品的销售单价不低于68元,日销售量与销售单价仍然满足(1)中的函数关系,若日销售最大利润是6600元,直接写出m的值.
【题目】在“新冠肺炎防控”知识宣传活动中,某社区对居民掌握新冠肺炎防控知识的情况进行调查.其中![]() 、
、![]() 两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
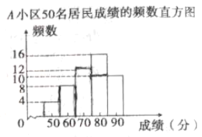
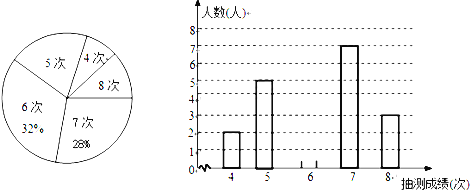
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
(信息二)图中,![]() 小区从左往右第四组的成绩如下
小区从左往右第四组的成绩如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 、
、![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 |
| 277 | |
| 75.1 | 77 | 76 |
| 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区500名居民中能超过平均数的有多少人?
小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析![]() ,
,![]() 两小区居民掌握新冠防控知识的情况.
两小区居民掌握新冠防控知识的情况.
【题目】阅读对学生的成长有着深远的影响.某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调查结果经制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合计 | 1 |
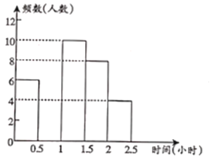
请根据图表中的信息,解答下列问题:
(1)表中的![]() ,
,![]() ,将频数分布直方图补全;
,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足1小时的学生大约有多少名?
(3)![]() 组的4人中,有1名男生和3名女生,该校计划在
组的4人中,有1名男生和3名女生,该校计划在![]() 组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.