Question

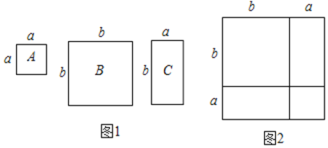
【题目】如图，在△ABC中，∠ACB=90°，AC=BC=10，在△DCE中，∠DCE=90°，DC=EC=6，点D在线段AC上，点E在线段BC的延长线上．将△DCE绕点C旋转60°得到△D′CE′（点D的对应点为点D′，点E的对应点为点E′），连接AD′、BE′，过点C作CN⊥BE′，垂足为N，直线CN交线段AD′于点M，则MN的长为_____．

Answer 1

【答案】7+或7﹣

【解析】

将△DCE绕点C旋转60°得到△D′CE′，可分为顺时针和逆时针旋转两个图形；先求顺时针旋转的情形，如图作辅助线，先解Rt△BFC，再解△BE′F求BE′，用“面积法”求CN，证明△ACG≌△BCN，△CD′H≌△CE′N，将有关线段转化，可求CM，从而可求MN．

若将△DCE绕点C顺时针旋转60°得到△D′CE′，

如图中左边所示，过点B作E′C的垂线交其延长线于F点，过点D′作CM的垂线交CM于H点，过A点作CM的垂线交其延长线于G点．

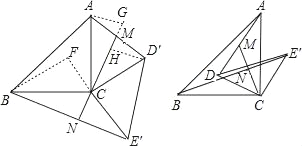
∵∠ACD′=60°，∠ACB=∠D′CE′=90°，

∴∠BCE′=360°﹣∠ACD′﹣∠ACB﹣∠D′CE′=120°．

∴∠BCF=180°﹣∠BCE′=60°，

BF=sin∠BCFBC=×10=5，

∴S△BCE′=BFCE′=15．

∵∠ACG+∠BCN=90°，∠BCN+∠CBN=90°，

∴∠ACG=∠CBN，

又∵AC=BC，

∴Rt△ACG≌Rt△CBN，

∴AG=CN，CG=BN．

同理△CD′H≌△E′CN，D′H=CN，CH=NE′．

∴AG=D′H，

在△AMG和△D′MH中，

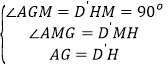
∴△AMG≌△D′MH，

∴HM=MG，

∴M为GH中点，CM=（CG+CH）=（NB+NE′）=BE′．

又∵BF=5，∠BCF=60°，

∴CF=5，FE′=CF+CE′=11，

∴BE′=，

∴CM=BE′=7．

又∵S△BCE′=CNBE′，

∴CN=2S△BCE′÷BE′=，

∴MN=CM+CN=7+．

②同理，当△CDE逆时针旋转60°时，MN如图中右边所示，MN=7﹣．

故答案为：7+或7﹣．