题目内容
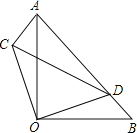
【题目】如图,△AOB,△COD是等腰直角三角形,点D在AB上.
(1)求证:△ACO≌△BDO;
(2)若∠BOD=30°,求∠ACD度数.
【答案】(1)证明见解析;(2)∠ACD=60°.
【解析】
(1)根据等腰直角三角形得出OC=OD,OA=OB,∠AOB=∠COD=90°,求出∠AOC=∠BOD,根据全等三角形的判定定理推出即可;
(2)根据全等三角形的性质求出∠BOD=∠ACO=30°,∠CAO=∠OBD=45°,然后利用三角形内角和求出∠ACO,进而求解.
解:(1)∵△AOB,△COD是等腰直角三角形,
∴OC=OD、AO=BO、∠COA+∠AOD=∠DOB+∠AOD=90°,
∴∠COA=∠DOB,
∴△ACO≌△BDO (SAS),
(2)解:∵△ACO≌△BDO,
∴∠BOD=∠ACO=30°,∠CAO=∠OBD=45°,
∴∠ACO=180°﹣30°﹣45°=105°,
∴∠ACD∠ACO﹣∠OCD=105°﹣45°=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目