题目内容
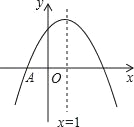
【题目】如图，抛物线y＝ax2+bx+c与x轴交于点A(﹣1，0)，顶点坐标(1，n)，与y轴的交点在(0，2)，(0，3)之间(包含端点)，则下列结论：①3a+b＜0；②﹣1≤a≤﹣
；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c＝n﹣1有两个不相等的实数根．其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
利用抛物线的开口方向可得a<0，再由抛物线的对称轴可得b=-2a，由此可对①进行判断；利用2≤c≤3结合已知条件可对②进行判断；利用二次函数的性质可对③进行判断；根据抛物线y＝ax2+bx+c直线y=n-1的交点个数可对④进行判断.
∵抛物线开口向下，
∴a<0，
∵抛物线的对称轴为直线x=
=1，
∴b=-2a，
∴3a+b=3a-2a=a<0，故①正确；
∵抛物线y＝ax2+bx+c与x轴交于点A(﹣1，0)，
∴a-b+c=0，∴c=-3a，
∵2≤c≤3，
∴2≤-3a≤3，
∴﹣1≤a≤﹣
，故②正确；
∵抛物线的顶点坐标为（1，n），
∴x=1时，二次函数有最大值为n，
∴对于任意实数m ，总有a+b+c≥am2+bm+c，
即a+b≥am2+bm，故③正确；
∵抛物线的顶点坐标为（1，n），
∴抛物线y＝ax2+bx+c直线y=n-1有两个交点，
∴关于x的方程ax2+bx+c＝n﹣1有两个不相等的实数根，故④正确，
故选D.
【题目】某企业生产了一款健身器材，可通过实体店和网上商店两种途径进行销售，销售了一段时间后，该企业对这种健身器材的销售情况进行了为期30天的跟踪调查，其中实体店的日销售量y1(套)与时间x(x为整数，单位:天)的部分对应值如下表所示:
时间x(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量y(套) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)求出y1与x的二次函数关系式及自变量x的取值范围
(2)若网上商店的日销售量y2(套)与时间x(x为整数，单位:天)的函数关系为
，则在跟踪调查的30天中，设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式；当x为何值时，日销售总量y达到最大，并写出此时的最大值.
【题目】如图1，点C是⊙O中直径AB上的一个动点，过点C作CD⊥AB交⊙O于点D，点M是直径AB上一固定点，作射线DM交⊙O于点N．已知AB=6cm，AM=2cm，设线段AC的长度为xcm，线段MN的长度为ycm．
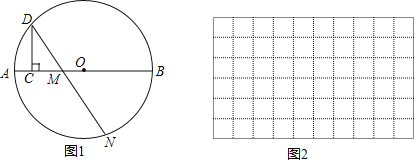
小东根据学习函数的经验，对函数y随自变量的变化而变化的规律进行了探索．
下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了与y的几组值，如下表：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4 | 3.3 | 2.8 | 2.5 | 2.1 | 2 |
（说明：补全表格时相关数值保留一位小数）
（2）在图2中建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当AC=MN时，x的取值约为 cm．
