Question

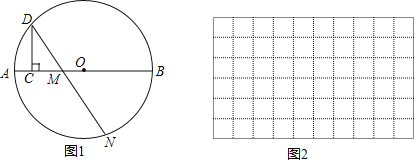
【题目】如图1，点C是⊙O中直径AB上的一个动点，过点C作CD⊥AB交⊙O于点D，点M是直径AB上一固定点，作射线DM交⊙O于点N．已知AB=6cm，AM=2cm，设线段AC的长度为xcm，线段MN的长度为ycm．

小东根据学习函数的经验，对函数y随自变量的变化而变化的规律进行了探索．

下面是小东的探究过程，请补充完整：

（1）通过取点、画图、测量，得到了与y的几组值，如下表：

x/cm	0	1	2	3	4	5	6
y/cm	4	3.3	2.8	2.5		2.1	2

（说明：补全表格时相关数值保留一位小数）

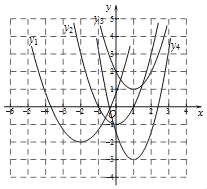
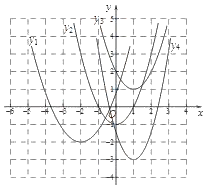
（2）在图2中建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

（3）结合画出的函数图象，解决问题：当AC=MN时，x的取值约为 cm．

Answer 1

【答案】（1）2.3；（2）见解析；（3）．

【解析】

（1）如图1中，连接OD，BD、AN．利用勾股定理求出DM，由相似三角形的性质求出MN即可；

（2）利用描点法画出函数图象即可；

（3）利用图象寻找图象与直线y=x的交点的坐标即可解决问题；

（1）如图1中，连接OD，BD、AN．

∵AC=4，OA=3，

∴OC=1，

在Rt△OCD中，CD=，

在Rt△CDM中，DM=，

由△AMN∽△DMB，可得DMMN=AMBM，

∴MN=≈2.3，

故答案为2.3．

（2）函数图象如图所示，

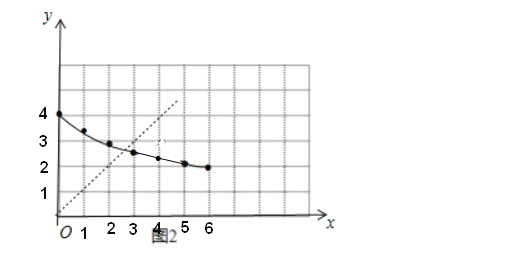
（3）观察图象可知，当AC=MN上，x的取值约为2.7．

故答案为2.7．