ƒøƒ⁄»ð
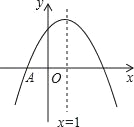
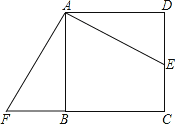
°æƒø°øƒ≥∆Û“µ…˙≤˙¡À“ªøÓΩ°…Ì∆˜≤ƒ£¨ø…Õ®π˝ µÃµÍ∫ÕÕ¯…œ…õ͡Ω÷÷Õææ∂Ω¯––œ˙ €£¨œ˙ €¡À“ª∂Œ ±º‰∫Û£¨∏√∆Û“µ∂‘’‚÷÷Ω°…Ì∆˜≤ƒµƒœ˙ €«ÈøˆΩ¯––¡ÀŒ™∆⁄30Ãϵƒ∏˙◊Ÿµ˜≤È£¨∆‰÷– µÃµ͵ƒ»’œ˙ €¡øy1(Ã◊)”Î ±º‰x(xŒ™’˚ ˝£¨µ•Œª:ÃÏ)µƒ≤ø∑÷∂‘”¶÷µ»Áœ¬±ÌÀ˘ æ:
±º‰x(ÃÏ) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
»’œ˙ €¡øy(Ã◊) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
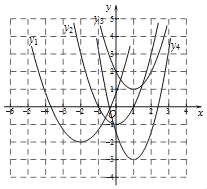
(1)«Û≥ˆy1”Îxµƒ∂˛¥Œ∫Ø ˝πÿœµ Ωº∞◊‘±‰¡øxµƒ»°÷µ∑∂Œß
(2)»ÙÕ¯…œ…õ͵ƒ»’œ˙ €¡øy2(Ã◊)”Î ±º‰x(xŒ™’˚ ˝£¨µ•Œª:ÃÏ)µƒ∫Ø ˝πÿœµŒ™![]() £¨‘Ú‘⁄∏˙◊Ÿµ˜≤ȵƒ30ÃÏ÷–£¨…Ë µÃµÍ∫ÕÕ¯…œ…õ͵ƒ»’œ˙ €◊СøŒ™y(Ã◊),«Ûy”Îxµƒ∫Ø ˝πÿœµ Ω£ªµ±xŒ™∫Œ÷µ ±£¨»’œ˙ €◊Сøy¥ÔµΩ◊Ó¥Û£¨≤¢–¥≥ˆ¥À ±µƒ◊Ó¥Û÷µ.
£¨‘Ú‘⁄∏˙◊Ÿµ˜≤ȵƒ30ÃÏ÷–£¨…Ë µÃµÍ∫ÕÕ¯…œ…õ͵ƒ»’œ˙ €◊СøŒ™y(Ã◊),«Ûy”Îxµƒ∫Ø ˝πÿœµ Ω£ªµ±xŒ™∫Œ÷µ ±£¨»’œ˙ €◊Сøy¥ÔµΩ◊Ó¥Û£¨≤¢–¥≥ˆ¥À ±µƒ◊Ó¥Û÷µ.
°æ¥∞∏°ø£®1£©![]() £¨£®0°Ðx°Ð30£¨«“Œ™’˚ ˝£©£ª£®2£©µ±x=30 ±£¨y»°µ√◊Ó¥Û÷µ360.
£¨£®0°Ðx°Ð30£¨«“Œ™’˚ ˝£©£ª£®2£©µ±x=30 ±£¨y»°µ√◊Ó¥Û÷µ360.
°æΩ‚Œˆ°ø
£®1£©…Ëy1=ax2+bx+c£¨»ª∫ÛÕ®π˝¥˝∂®œµ ˝∑®«Û≥ˆy1”Îxµƒ∫Ø ˝πÿœµ Ω£ª
£®2£©“¿Ã‚“‚”–y=y1+y2£¨∏˘æð◊‘±‰¡øµƒ≤ªÕ¨«¯º‰∑÷±µ√µΩ∂‘”¶µƒ∂˛¥Œ∫Ø ˝Ω‚Œˆ Ω£¨‘⁄∏˜◊‘«¯º‰ƒ⁄«Û≥ˆ∆‰◊Ó¥Û÷µ£¨◊Ó∫Û±»Ωœµ√≥ˆ¡Ω÷÷«¯º‰∑∂Œßƒ⁄µƒ◊Ó¥Û÷µ.
£®1£©y1=ax2+bx+c£¨Ω´£®0,0£©,£®5,25£©,£®10,40£©¥˙»Îø…µ√
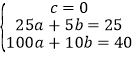 £¨Ω‚µ√
£¨Ω‚µ√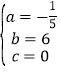 £¨
£¨
°ý![]() £¨£®0°Ðx°Ð30£¨«“Œ™’˚ ˝£©£ª
£¨£®0°Ðx°Ð30£¨«“Œ™’˚ ˝£©£ª
£®2£©“¿Ã‚“‚”–y=y1+y2£¨
µ±0°Ðx°Ð10 ±£¨
![]()
![]() ,
,
°ýµ±x=10 ±£¨y»°µ√◊Ó¥Û÷µ80£ª
µ±10<x°Ð30 ±£¨
![]()
![]()
°ýµ±x=30 ±£¨y»°µ√◊Ó¥Û÷µ360£ª
◊€…œø…÷™£¨µ±x=30 ±£¨y»°µ√◊Ó¥Û÷µ360.

 ƒÐøº ‘∆⁄ƒ©≥Â¥ÃæÌœµ¡–¥∞∏
ƒÐøº ‘∆⁄ƒ©≥Â¥ÃæÌœµ¡–¥∞∏°æƒø°øŒ“ –ƒ≥÷–—ß柖–°∞÷–π˙√Œ–£‘∞∫√…˘“Ù°±∏Ë ÷¥Û»¸£¨∏þ°¢≥ı÷–≤ø∏˘æð≥ı»¸≥…º®£¨∏˜—°≥ˆ5√˚—° ÷◊È≥…≥ı÷–¥˙±Ì∂”∫Õ∏þ÷–¥˙±Ì∂”≤Œº”—ß–£æˆ»¸£Æ¡Ω∏ˆ∂”∏˜—°≥ˆµƒ5√˚—° ÷µƒæˆ»¸≥…º®»ÁÕºÀ˘ æ£Æ

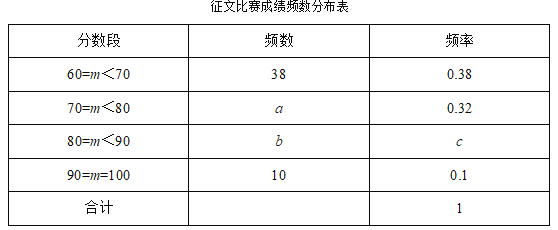
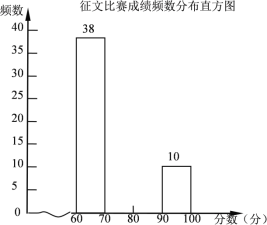
£®1£©∏˘æðÕº æÃÓ–¥œ¬±Ì£ª
∆Ωæ˘ ˝£®∑÷£© | ÷–Œª ˝£®∑÷£© | ÷⁄ ˝£®∑÷£© | |
≥ı÷–≤ø | 85 | ||
∏þ÷–≤ø | 85 | 100 |
£®2£©Ω·∫œ¡Ω∂”≥…º®µƒ∆Ωæ˘ ˝∫Õ÷–Œª ˝£¨∑÷Œˆƒƒ∏ˆ∂”µƒæˆ»¸≥…º®Ωœ∫√£ª
£®3£©º∆À„¡Ω∂”戻¸≥…º®µƒ∑Ω≤Ó≤¢≈–∂œƒƒ“ª∏ˆ¥˙±Ì∂”—° ÷≥…º®ΩœŒ™Œ»∂®£Æ