题目内容
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求sinE的值.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)要证明是圆的切线,须证明过切点的半径垂直,所以连接OB,证明OB⊥PE即可.
(2)要求sinE,首先应找出∠E所在的直角三角形,然后利用直角三角函数求解即可.而sinE既可放在直角三角形EAP中,也可放在直角三角形EBO中,所以利用相似三角形的性质求出EP或EO的长即可解决问题
(1)证明:连接OB
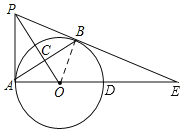
∵PO⊥AB,
∴AC=BC,
∴PA=PB,
在△PAO和△PBO中
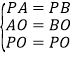 ,
,
∴△PAO和≌△PBO,
∴∠OBP=∠OAP=90°,
∴PB是⊙O的切线.
(2)连接BD,则BD∥PO,且BD=2OC=6
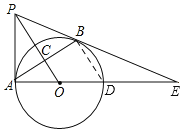
在Rt△ACO中,OC=3,AC=4
∴AO=5
在Rt△ACO与Rt△PAO中,
∠APO=∠APO,
∠PAO=∠ACO=90°
∴△ACO△PAO
∴![]()
∴PO=![]() ,PA=
,PA=![]()
∴PB=PA=![]()
在△EPO与△EBD中,
BD∥PO
∴△EPO∽△EBD
∴![]() ,
,
解得EB=![]() ,PE=
,PE=![]() ,
,
∴sinE=![]() .
.

练习册系列答案
相关题目
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
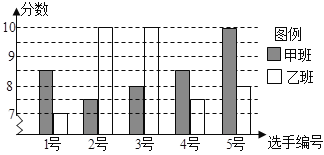
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.