题目内容
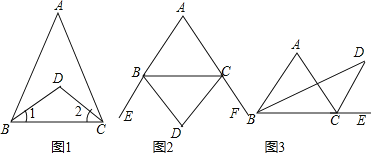
【题目】（1）阅读并填空：如图①，BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线．
试说明∠D=90°+
∠A的理由．
解：因为BD平分∠ABC（已知），
所以∠1= （角平分线定义）．
同理：∠2= ．
因为∠A+∠ABC+∠ACB=180°，∠1+∠2+∠D=180°，（ ），
所以∠D = （等式性质）．
即：∠D=90°+∠A．
（2）探究，请直接写出结果，并任选一种情况说明理由：
（i）如图②，BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线．试探究∠D与∠A之间的等量关系．
答：∠D与∠A之间的等量关系是 ．
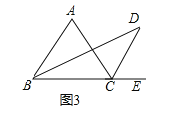
（ii）如图③，BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线．试探究∠D与∠A之间的等量关系．
答：∠D与∠A之间的等量关系是 ．
【答案】（1）
∠ABC；∠ACB；三角形的内角和等于180°；∠D=180°﹣（∠ABC+∠ACB）；（2）∠D=90°﹣∠A；∠D=∠A
【解析】试题分析：（1）、（2）、（3）关键“三角形的一个内角等于和它不相邻的两个外角的和”、“三角形的内角和等于180°”及等式的性质分析求解．试题解析：（1）阅读并填空：如图①，BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线．
试说明∠D=90°+∠A的理由．
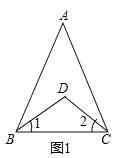
解：因为BD平分∠ABC（已知），
所以∠1= ∠ABC （角平分线定义）．
同理：∠2= ∠ACB ．
因为∠A+∠ABC+∠ACB=180°，∠1+∠2+∠D=180°，（ 三角形的内角和等于180° ），
所以 ∠D=180°﹣（∠ABC+∠ACB） （等式性质）．
即：∠D=90°+∠A．
（2）探究，请直接写出结果，无需说理过程：
（i）如图②，BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线．试探究∠D与∠A之间的等量关系．
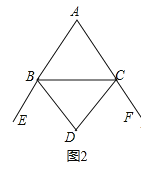
答：∠D与∠A之间的等量关系是 ∠D=90°﹣∠A ．
（ii）如图③，BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线．试探究∠D与∠A之间的等量关系．
答：∠D与∠A之间的等量关系是 ∠D=∠A ．（每空1分）
（2）解：（i）∠D与∠A之间的等量关系是：∠D=90°﹣∠A．
理由：∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线，
∴∠EBD=∠DBC，∠BCD=∠DCF，
∴∠DBC+∠DCB+∠D=180°，
∴∠A+∠ABC+∠ACB=180°，
而∠ABC=180°﹣2∠DBC，
∠ACB=180°﹣2∠DCB，
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°，
∴∠A﹣2（∠DBC+∠DCB）=﹣180°，
∴∠A﹣2（180°﹣∠D）=﹣180°，
∴∠A﹣2∠D=180°，
∴∠D=90°﹣∠A
（ii）∠D与∠A之间的等量关系是：∠D=∠A．
理由：∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线，
∴∠DCE=∠DBC+∠D，
∵∠A+2∠DBC=2∠DCE
∴∠A+2∠DBC=2∠DBC+2∠D
∴∠A=2∠D
即：∠D=∠A
