题目内容
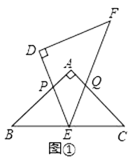
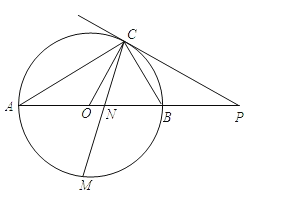
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是![]() 的中点,CM交AB于点N,若AB=6,求MNMC的值.
的中点,CM交AB于点N,若AB=6,求MNMC的值.
【答案】(1)详见解析;(2)18
【解析】
(1)已知C在圆上,故只需证明OC与PC垂直即可,根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP,故PC是⊙O的切线;
(2)连接MA,MB,由圆周角定理可得∠ABM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC,代入数据可得MNMC= BM2=18.
(1)证明:∵∠COB=2∠PCB,∠COB=2∠A,
∴∠A=∠PCB,
又∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠CBA=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠PCB+∠OCB=90°,即OC⊥CP,
∵OC是⊙O的半径,
∴PC是⊙O的切线;
(2)连接MA、MB,
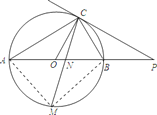
∵点M是![]() 的中点,
的中点,
∴∠ABM=∠BCM,
又∵∠BMN=∠CMB,
∴△MBN∽△MCB,
∴![]() ,即MN·MC=MB2,
,即MN·MC=MB2,
又∵AB是⊙O的直径且点M是![]() 的中点,
的中点,
∴∠AMB=90°且AM=BM,
∵AB=6,
∴BM=AM=![]() ,
,
∴MN·MC=BM2=18.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案【题目】水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的部分数据如下表:
销售时间t(1≤t≤15,t为整数)(天) | 1 | 4 | 5 | 8 | 12 |
销售单价p(元/千克) | 20.25 | 21 | 21.25 | 22 | 23 |
已知p与t之间的变化规律符合一次函数关系.
(1)试求p关于t的函数表达式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=-2t+120(1≤t≤15,t为整数).
① 求销售过程中最大日销售利润为多少?
② 在实际销售的前12天中,公司决定每销售1千克水果就捐赠n元利润(n<3)给“精准扶贫”对象.现发现:在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围
【题目】甲、已两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按![]() 折出售,乙商场对一次购物中超过200元后的价格部分打
折出售,乙商场对一次购物中超过200元后的价格部分打![]() 折. 设原价购物金额累计为
折. 设原价购物金额累计为![]() 元(
元(![]() ).
).
![]() 根据题意,填写下表: (单位:元)
根据题意,填写下表: (单位:元)
原价购物金额累计/元. | 130 | 300 | 700 | ··· |
甲商场实际购物金额/元 | 104 | 560 | ··· | |
乙商场实际购物金额/元 | 130 | 270 | ··· |
![]() 设在甲商场实际购物金额为
设在甲商场实际购物金额为![]() 元,在乙商场实际购物金额为
元,在乙商场实际购物金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
![]() 根据题意填空:
根据题意填空:
①若在同甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为______元 ;
②若在同一商场购物,商品原价购物金额累计为![]() 元,则在甲、乙.两家商场中的 商场实际购物花费金少.
元,则在甲、乙.两家商场中的 商场实际购物花费金少.
③若在同一商场实际购物金额为![]() 元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.