题目内容
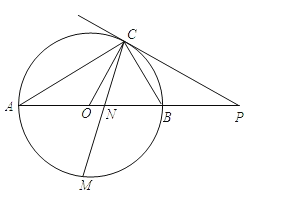
【题目】已知:如图,在![]() 中,
中,![]() 是AC中点,BE平分
是AC中点,BE平分![]() 交AC于点E,点O是AB上一点,
交AC于点E,点O是AB上一点,![]() 过B、E两点,交BD于点G,交AB于点
过B、E两点,交BD于点G,交AB于点![]() ,
,![]() 则下面结论正确的有
则下面结论正确的有![]() 填序号
填序号![]() ______(1)
______(1)![]() 与
与![]() 相切;(2)
相切;(2)![]() ;(3)
;(3)![]() 的直径等于8;(4)
的直径等于8;(4)![]() AE
AE

【答案】(1)(2)
【解析】
(1)正确.欲证明AC是切线,只要证明OE⊥AC,只要证明OE∥BD即可.
(2)正确.根据等弧所对的弦相等证明即可.
(3)错误.在Rt△BCD中,由![]() ,求出BC=BA=10,CD=AD=8,由EM⊥BF,ED⊥BD,∠EBM=∠EBD,推出EM=ED,设EM=ED=x,在Rt△AEM中,
,求出BC=BA=10,CD=AD=8,由EM⊥BF,ED⊥BD,∠EBM=∠EBD,推出EM=ED,设EM=ED=x,在Rt△AEM中,![]() ,列出方程求出x,再利用相似三角形的性质求出FM即可解决问题.
,列出方程求出x,再利用相似三角形的性质求出FM即可解决问题.
(4)错误.假设成立,推出矛盾即可.
解:如图连接EO,EF,作EM⊥AB于M.
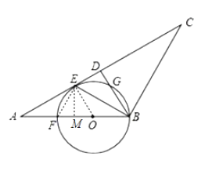
∵OE=OB,
∴∠OEB=∠OBE,
∵BE平分∠ABD,
∴∠ABE=∠EBD=∠OEB
∴OE//BD
∵AD=CD,BA=BC,
∴BD⊥AC
∴OE⊥AC
又∵OE是![]() 的半径
的半径
∴AC是⊙O的切线,故(1)正确.
∵∠EBF=∠EBG,
∴弧EF=弧EG.
∴EF= EG,故(2)正确.
在Rt△BCD中, BD=6,sinC=![]()
∴BC=BA=10,CD=AD=8,
∵EM⊥BF,ED⊥BD,∠EBM=∠EBD,
∴EM=ED,设EM=ED=x,
在Rt△AEM中,![]()
∴![]()
∴x=3,
∵∠EFM+∠FEM=90°,∠FEM+∠BEM=90°,
∴∠EFM=∠BEM,
∵∠EMF=∠EMB,
∴△EMF∽△BME,
∴![]()
∴![]()
∴![]()
∴BF=FM+BM=![]() ,
,
∴![]() 的直径等于
的直径等于![]() ,故(3)错误,
,故(3)错误,
设![]()
即![]()
∵∠A=∠A,
∴△ABE∽△ACB,
∴∠C=∠ABE
∵∠CBD=2∠ABE
∴∠CBD=2∠C
∵∠C+∠CBD=90°
∴∠C=30°
∵![]()
∴![]()
显然不符合题意,故(4)错误
故答案为(1)(2)

 名校通行证有效作业系列答案
名校通行证有效作业系列答案