题目内容
【题目】已知,在△ABC中,∠ABC=90°
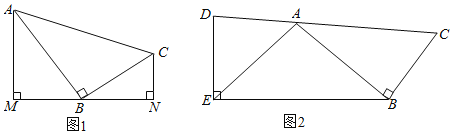
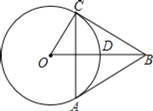
(1)如图1,分别过A、C两点作经过点B的直线MN的垂线,垂足分别为M、N.
①求证:△AMB∽△BNC;
②若△AMB∽△ABC,求证:AC=AM+CN;
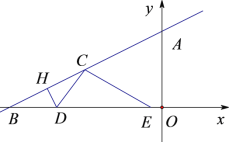
(2)如图2,点D是CA延长线上的一点,DE⊥EB,AE=AB,AD:BC:CA=3:3:5,求![]() 的值.
的值.
【答案】(1)①见解析,②见解析;(2)![]()
【解析】
(1)①根据同角的余角相等得到∠BAM=∠CBN,根据两角相等的两个三角形相似证明结论;
②作BH⊥AC,证明△BAM≌△BAH,根据全等三角形的性质得到AH=AM,同理得到CH=CN,证明结论;
(2)过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,根据平行线分线段成比例定理得到![]() ,根据△AGB∽△BHC,得到
,根据△AGB∽△BHC,得到![]() ,计算即可.
,计算即可.
(1)①∵∠ABC=90°,
∴∠ABM+∠CBN=90°,
∵AM⊥BM,
∴∠ABM+∠BAM=90°,
∴∠BAM=∠CBN,
∵∠BAM=∠CBN,∠AMB=∠BNC=90°,
∴△AMB∽△BNC;
②如图1,作BH⊥AC于H,
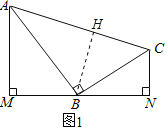
则∠AHB=∠ABC=90°,又∠BAH=∠CAB,
∴△AHB∽△ABC,
∵△AMB∽△ABC,
∴△AMB∽△AHB,
∴∠BAM=∠BAH,
在△BAM和△BAH中,
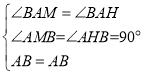 ,
,
∴△BAM≌△BAH(AAS)
∴AH=AM,
同理可证,CH=CN,
∴AC=AH+CH=AM+CN;
(2)如图2,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,
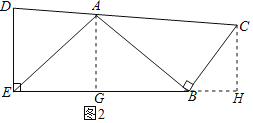
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]() ,
,
在Rt△ABC中,![]() ,
,
∴![]() ,
,
由(1)①可知,△AGB∽△BHC
∴![]() ,
,
∵AE=AB,AG⊥BE,
∴EG=GB,
∵![]() ,
,
∴EG:BG:BH=3:3:2,
设EG=3a,则BG=3a,BH=2a,
∵![]() ,
,
∴![]() ,
,
解得,![]() ,
,
由勾股定理得,![]() ,
,
∴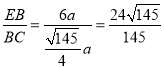 .
.

 名校课堂系列答案
名校课堂系列答案【题目】我们把图1称为一个基本图形,显然这个基本图形中有6个矩形,将此基本图形不断复制并向上平移、叠加,这样得到图2,图3…(如图所示)
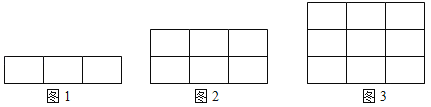
(1)观察图形,完成如表:
图形名称 | 矩形个数 |
图1 | 6 |
图2 | 18 |
图3 | 36 |
图4 | 60 |
图5 |
|
(2)根据以上规律猜想,图形n中共有多少个矩形(用含n的代数式表示)?