题目内容
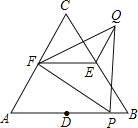
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,四边形PDEF是矩形,PD=2,PF=4,DE与AB边交于点G,点P从点B出发沿BC以每秒1个单位长的速度向点C匀速运动,伴随点P的运动,矩形PDEF在射线BC上滑动;点Q从点P出发沿折线PD﹣DE以每秒1个单位长的速度匀速运动.点P,Q同时出发,当点Q到达点E时停止运动,点P也随之停止.设点P,Q运动的时间是t秒(t>0)
(1)当t=1时,QD= ,DG= ;
(2)当点Q到达点G时,求出t的值;
(3)t为何值时,△PQC是直角三角形?
【答案】(1)1,![]() ;(2)∴t=
;(2)∴t=![]() s时,点Q到达点G;(3)当0<t≤2或t=3或t=4时,△PCQ是直角三角形.
s时,点Q到达点G;(3)当0<t≤2或t=3或t=4时,△PCQ是直角三角形.
【解析】
第一问根据相似的比例关系求解,第二问列方程形成等式,使Q到达G点,从而求出t,第三问根据△PCQ是直角三角形时,△QHP∽△CHQ,进而求出t.
(1)如图1中,设BG交PD于点K.
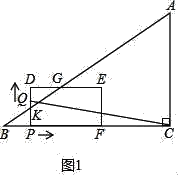
t=1时,PB=PQ=1,
∴DQ=1,
∵tan∠KBP=![]() =
=![]() ,
,
∴PK=![]() ,DK=
,DK=![]() ,
,
∵DG∥PB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DG=![]() ,
,
故答案为1,![]() .
.
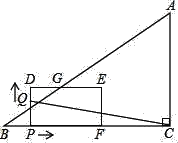
(2)当t=0时,DG=PD![]() =
=![]() ,
,
点Q到达点G时:t﹣2=![]() ﹣t,解得t=
﹣t,解得t=![]() ,
,
∴t=![]() s时,点Q到达点G.
s时,点Q到达点G.
(3)①当点Q在PD上时,即0<t≤2时,△QPC是直角三角形(∠QPC=90°)
②如图2中,当点Q在线段DE上时,作QH⊥PC于H.
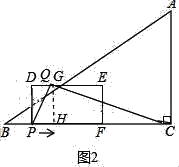
当∠PQC=90°时,△QHP∽△CHQ,
可得QH2=PHHC,
∴22=(t﹣2)(8﹣t﹣t+2),
解得t=3或4,
∴t=3或4时,∠PQC=90°,
综上所述,当0<t≤2或t=3或t=4时,△PCQ是直角三角形.

【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.