题目内容
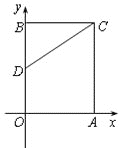
【题目】如图,已知一次函数![]() 与两坐标分别交于
与两坐标分别交于![]() 两点,动点
两点,动点![]() 从原点
从原点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 轴正方向运动,连接
轴正方向运动,连接![]() .设运动时间为
.设运动时间为![]() s.
s.
(1)当![]() 为何值时,
为何值时,![]() 的面积为6?
的面积为6?
(2)若![]() ,作
,作![]() 中边
中边![]() 上的高
上的高![]() ,当
,当![]() 为何值时,
为何值时,![]() 长为4?并直接写出此时点
长为4?并直接写出此时点![]() 的坐标.
的坐标.

【答案】(1) ![]() 或
或![]() ;(2)
;(2) ![]()
![]() .
.
【解析】
(1)先求出A、B两点的坐标,再分点P在B点左侧与右侧两种情况进行讨论即可;
(2)作△PAB中AP边上的高BQ,先根据AAS得出△AOP≌△BQP,再由勾股定理得出t的值,继而得出结论即可.
(1)当x=0时,![]() =4,
=4,
当y=0时,0=![]() ,解得:x=8,
,解得:x=8,
∴A(0,4),B(8,0),
即AO=4,OB=8,
∵△PAB的面积为6,
∴![]() PBAO=6,
PBAO=6,
∴PB=3,
∵OP=2t,
∴当点P在点B的左侧时,PB=8-2t;当点P在点B的右侧时,PB=2t-8;
即8-2t=3或2t-8=3,
∴![]() 或
或![]() ;
;
(2) 作△PAB中AP边上的高BQ,
在△AOP和△BQP中
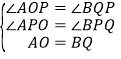 ,
,
∴△AOP≌△BQP,
∴AP=BP,
在Rt△AOP中,OP2+OA2=AP2,
即42+(2t)2=(8-2t)2,
解得t=![]() ,
,
∴当t=![]() 时,BQ的长为4,
时,BQ的长为4,
作QH⊥OB于H,则有HQ//OA,
∴△PHQ∽△POA,
∴![]() ,
,
∴![]() ,
,
∴HQ=![]() ,PH=
,PH=![]() ,
,
∴OH=OP+PH=![]() ,
,
∴Q![]() .
.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目