题目内容
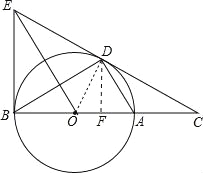
【题目】如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.

(1)求证:CD是⊙O的切线;
(2)若BC=8cm,tan∠CDA=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)条件下,过点B作⊙O的切线交CD的延长线于点E,连接OE,求四边形OEDA的面积.
【答案】(1)证明见解析(2)3(3)12.6
【解析】
试题分析:(1)要证明CD是⊙O的切线,只需要连接OD,证明∠ODC=90°即可,由∠CDA=∠CBD,∠BDA=90°,OA=OD得到∠ODA=∠OAD,然后进行转化即可得到∠ODC=90°,本题得以解决;
(2)根据题意可以得到△CDA和△CBD相似,然后根据BC=8cm,tan∠CDA=![]() ,∠CDA=∠CBD,可以求得CD、CA的长,从而可以求得BA的长,进而可以得到⊙O的半径;
,∠CDA=∠CBD,可以求得CD、CA的长,从而可以求得BA的长,进而可以得到⊙O的半径;
(3)由题意可得,∠EBC=90°,可以证明△EBC和△ODC相似,从而可以求得EB的长,然后根据四边形OEDA的面积等于△EBC的面积减去△EBO的面积再减去△DAC的面积,从而可以得到四边形OEDA的面积,本题得以解决.
试题解析:(1)连接OD,如右图所示,
∵AB为⊙O的直径,
∴∠BDA=90°,
又∵OD=OA,∠CDA=∠CBD,
∴∠ODA=∠OAD,
∴∠CBD+∠OAD=180°﹣∠BDA=90°,
∴∠ODA+∠CDA=∠OAD+∠CDA=90°,
∴∠ODC=90°,
即CD是⊙O的切线;
(2)∵∠DCA=∠BCD,∠CDA=∠CBD,
∴△CDA∽△CBD,
∴![]() ,
,
又∵BC=8cm,tan∠CDA=![]() ,∠CDA=∠CBD,∠BDA=90°,
,∠CDA=∠CBD,∠BDA=90°,
∴tan∠CBD=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得,CD=4,CA=2,
∴BA=CB﹣CA=8﹣2=6,
∴OB=3,
即⊙O的半径是3cm;
(3)作DF⊥BC于点F,如右上图所示
由已知可得,∠ODC=∠EBC=90°,∠DCO=∠BCE,
∴△DCO∽△BCE,
∴![]() ,
,
∵OD=3,CD=4,CB=8,
∴EB=6,
又∵CO=CB﹣OB=8﹣3=5,OD=3,CD=4,∠ODC=90°,DF⊥OC,
∴![]() ,
,
解得DF=2.4,
∴![]() =
=![]() =
=![]() =12.6cm,
=12.6cm,
即四边形OEDA的面积是12.6cm2.

 名校课堂系列答案
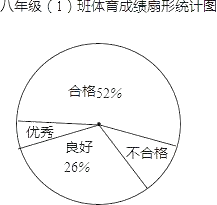
名校课堂系列答案【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .