题目内容
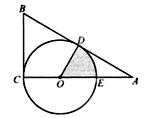
【题目】如图，已知AC是⊙O的直径，点B在圆周上（不与A、C重合），点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（ ）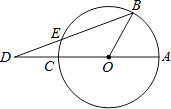 
A.DE=EB
B.
DE=EB
C.
DE=DO
D.DE=OB
【答案】D
【解析】解：连接EO． ∵OB=OE，
∴∠B=∠OEB，
∵∠OEB=∠D+∠DOE，∠AOB=3∠D，
∴∠B+∠D=3∠D，
∴∠D+∠DOE+∠D=3∠D，
∴∠DOE=∠D，
∴ED=EO=OB，
故选D．
A、错误．假设DE=EB，则△EOB是等边三角形，则∠AOB=3∠D=90°，OB⊥AD，显然与题目不符．
B、错误．假设 
DE=EB，则△EOB是等腰直角三角形，则∠AOB=3∠D=67.5°，显然与题目不符．
C、错误．假设 
DE=EB，则△EOB是等腰三角形，且底角∠B=30°，则∠AOB=45°，显然不符合题意．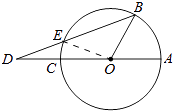
连接EO，只要证明∠D=∠EOD即可解决问题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
