题目内容
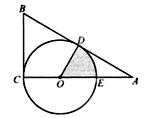
【题目】如图， 
为 
的直角边 
上一点，以 
为半径的 
与斜边 
相切于点 
，交 
于点 
．已知 
， 
．
（1）求 
的长；
（2）求图中阴影部分的面积．
【答案】
（1）
解：在Rt△ABC中，AB=
=
=2 
.
∵BC⊥OC
∴BC是⊙O的切线
又∵AB是⊙O的切线
∴BD=BC=
∴AD=AB-BD=
（2）
解：在Rt△ABC中，sinA= 
=
=
.
∴∠A=30°.
∵AB切⊙O于点D.
∴OD⊥AB.
∴∠AOD=90°-∠A=60°.
∵ 
=tanA=tan30°.
∴ 
=
.
∴OD=1.
S阴影=
=
.
【解析】（1）在Rt△ABC中，利用勾股定理求出AB的长，然后根据切线的判定证出BC为切线，然后可根据切线长定理可求解.
（2）在Rt△ABC中，根据∠A的正弦求出∠A度数，然后根据切线的性质求出OD的长，和扇形圆心角的度数，再根据扇形的面积公式可求解.
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键．
【题目】为降低空气污染，启东飞鹤公交公司决定全部更换节能环保的燃气公交车．计划购买A型和B型两种公交车共10辆，其中每台的价格，年载客量如表：
A型 | B型 | |
价格（万元/台） | a | b |
年载客量（万人/年） | 60 | 100 |
若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求a，b的值；
（2）如果该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次．请你设计一个方案，使得购车总费用最少．
【题目】为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费．如表所 示是该市居民“一户一表”生活用水及提示计费价格表的部分信息：
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价：元/ 吨 | 单价：元/ 吨 |
17 吨以下 | a | 0.80 |
超过 17 吨但不超过 30 吨的部分 | b | 0.80 |
超过 30 吨的部分 | 6.00 | 0.80 |
（说明：①每户产生的污水量等于该户自来水用水量；②水费自来水费用 污水处理费用）
已知小明家 2017 年 5 月份用水 20 吨，交水费 66 元；6 月份用水 25 吨交水费91元；
（1）求a 、b 的值；
（2）为了节约开支，小明家计划把 7 月份的水费控制在不超过家庭月收入的2% ．若小明家的月收入为 9200 元，则小明家 7 月份最多能用水多少吨？
