题目内容
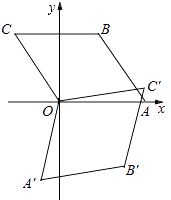
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣ ![]() x2+
x2+ ![]() x+4经过A、B两点.
x+4经过A、B两点.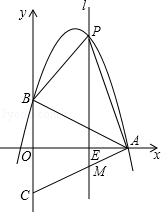
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:抛物线y=﹣ ![]() x2+
x2+ ![]() x+4中:
x+4中:
令x=0,y=4,则 B(0,4);
令y=0,0=﹣ ![]() x2+
x2+ ![]() x+4,解得 x1=﹣1、x2=8,则 A(8,0);
x+4,解得 x1=﹣1、x2=8,则 A(8,0);
∴A(8,0)、B(0,4)
(2)
解:△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,﹣4).
由A(8,0)、B(0,4),得:直线AB:y=﹣ ![]() x+4;
x+4;
依题意,知:OE=2t,即 E(2t,0);
∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;
S=S△ABC+S△PAB= ![]() ×8×8+
×8×8+ ![]() ×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;
×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;
∴当t=2时,S有最大值,且最大值为64
(3)
解:∵PM∥y轴,∴∠AMP=∠ACO<90°;
而∠APM是锐角,所以△PAM若是直角三角形,只能是∠PAM=90°;
由A(8,0)、C(0,﹣4),得:直线AC:y= ![]() x﹣4;
x﹣4;
所以,直线AP可设为:y=﹣2x+h,代入A(8,0),得:
﹣16+h=0,h=16
∴直线AP:y=﹣2x+16,联立抛物线的解析式,得:
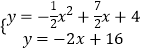 ,解得
,解得 ![]() 、
、 ![]()
∴存在符合条件的点P,且坐标为(3,10).

【解析】(1)抛物线的解析式中,令x=0,能确定点B的坐标;令y=0,能确定点A的坐标.(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由( ![]() PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为﹣1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标.
PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为﹣1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?