题目内容
【题目】换个角度看问题.
(原题重现)
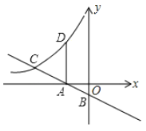
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
……
若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
(问题再研)
若设慢车行驶的时间为x(h),慢车与甲地的距离为s1(km),第一列快车与甲地的距离为s2(km),第二列快车与甲地的距离为s3(km),根据原题中所给信息解决下列问题:
(1)在同一直角坐标系中,分别画出s1、s2与x之间的函数图象;
(2)求s3与x之间的函数表达式;
(3)求原题的答案.
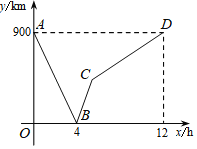
【答案】(1)s1=900﹣75x(0≤x≤12),s2=150x(0≤x≤6),图见解析;(2)s3=150x﹣112.5;(3)第二列快车比第一列快车晚出发0.75小时.
【解析】
(1)根据题意和函数图象中的数据可以分别求得s1、s2与x之间的函数关系式,从而可以可以画出s1、s2与x之间的函数图象;
(2)根据题意和(1)中的函数关系式可以求得s3与x之间的函数表达式;
(3)根据(2)中函数关系式,令s3=0求出相应的x的值,即可解答本题.
(1)慢车速度为:900÷12=75km/h,
则快车速度为:(900﹣75×4)÷4=150km/h,
则s1=900﹣75x(0≤x≤12),s2=150x(0≤x≤6),
则s1、s2与x之间的函数图象如图所示;

(2)由(1)知s1=900﹣75x,
当x=4.5时,s1=562.5,
设s3与x之间的函数表达式为s3=150x+b,
当x=4.5时,s3=562.5,
562.5=150×4.5+b,得b=﹣112.5,
即s3=150x﹣112.5;
(3)∵s3=150x﹣112.5,
∴当s3=0时,x=0.75,
即第二列快车比第一列快车晚出发0.75小时.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案