Question

【题目】某班老师要求每人每学期读4~7本书，并随机抽查了本学期学生读课外书册数的情况，绘制成不完整的条形图和不完整的扇形图，其中条形图被墨迹遮盖了一部分，回答下列问题：

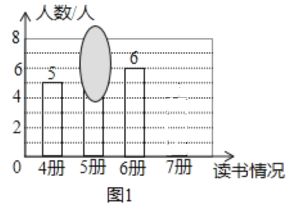
（1）请你求出老师随机抽查了多少名学生；

（2）已知册数的中位数是5，

嘉嘉说：条形图中被遮盖的数为5

淇淇说：条形图中被遮盖的数为6

ⅰ你认为嘉嘉和淇淇谁说的正确，请说明原因，并把条形图补充完整；

ⅱ在扇形图中，“7册”部分所对的圆心角为_______°，并把扇形图补充完整；

（3）请直接写出：从抽查学生中任取两人，恰好都读7册书的概率为_______．

Answer 1

【答案】（1）老师随机抽查了20名学生；（2）ⅰ淇淇说的正确，说明原因见解析；条型图见解析；ⅱ54，扇形图见解析；（3）．

【解析】

（1）利用4册的频数和百分比即可得到总人数；

（2）i根据两个人的说法分别求中位数，若得到中位数是5即是正确，否则错误；

ⅱ用7册的数量除以总数20再乘以360°即可得到；

（3）20个人中设1、2、3每人读7册，每个人只能与另一个人被同时抽查，由此得到所有可能的情况，再列举同时抽查2个人的情况，即可利用概率公式计算得到答案.

（1）人，

∴老师随机抽查了多少名学生；

（2）ⅰ淇淇说的正确，

如果条形图中被遮盖的数为5，则册数的中位数是5.5，不符合题意；

如果条形图中被遮盖的数为6，则册数的中位数是5，

故淇淇说的正确；

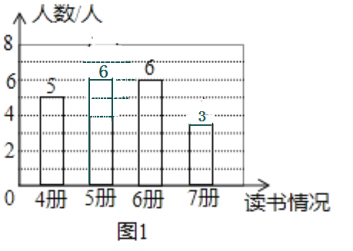
7册的数量是：20-5-6-6=3（人），

条形图如下：

ⅱ“7册”部分的圆心角度数是，

故答案为：54

（3）20个人中设1、2、3每人读7册，

∵每个人只能与另一个人被同时抽查，

∴共有种可能的情况，

同时抽查2个人的情况有：（1,2），（1,3），（2,1），（2,3），（3,1），（3,2）共6种，

∴从抽查学生中任取两人，恰好都读7册书的概率为，

故答案为： .