Question

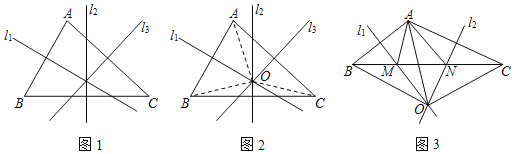
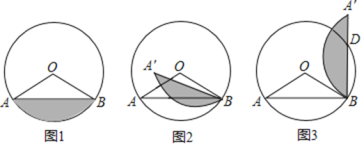
【题目】如图1、图2，在圆O中，，，将弦AB与弧AB所围成的弓形包括边界的阴影部分绕点B顺时针旋转度，点A的对应点是．

点O到线段AB的距离是______；______；点O落在阴影部分包括边界时，的取值范围是______；

如图3，线段B与优弧ACB的交点是D，当时，说明点D在AO的延长线上；

当直线与圆O相切时，求的值并求此时点运动路径的长度．

Answer 1

【答案】(1)；120；；(2)见解析;(3)或;,.

【解析】

利用垂径定理和特殊角的三角函数值解答；当与OB重叠时，取最小值；当OB绕点B顺时针旋转至与圆相交时，交点为，来求的最大值；

连接AD，利用圆周角定理进行证明；

利用切线的性质求得的值，并利用弧长公式求得相应的点运动路径的长度．

解：如图1，过点O作于点D，

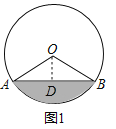
由垂径定理知，，
又，
，
．
又，
．
如图2，当与OB重叠时，；

当OB绕点B顺时针旋转至与圆相交，交点为，连接，则，此时是等边三角形，
，
的取值范围是：．
故答案是：；120；；
连接AD，，

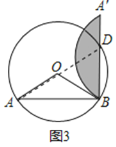
为直径，
所以D在AO的延长线上；
当与相切，
，
此时
或
或
当时，
运动路径的长度
当时，
运动路径的长度．