题目内容
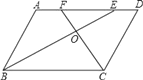
【题目】一张长方形纸片的长为m,宽为n(m>3n)如图1,先在其两端分别折出两个正方形(ABEF、CDGH)后展开(如图2),再分别将长方形ABHG、CDFE对折,折痕分别为MN、PQ(如图3),则长方形MNQP的面积为( )

A.n2B.n(m﹣n)C.n(m﹣2n)D.![]()
【答案】A
【解析】
由折叠可得,AF=AB=CD=GD=n,进而得到FG=m﹣2n,AG=DF=m﹣n,由折叠可得,DP=![]() DF=
DF=![]() (m﹣n),AM=
(m﹣n),AM=![]() AG=
AG=![]() (m﹣n),即可得到MP=AD﹣AM﹣DP=m﹣2×
(m﹣n),即可得到MP=AD﹣AM﹣DP=m﹣2×![]() (m﹣n)=n,再根据MN=PQ=n,即可得出长方形MNQP的面积为n2.
(m﹣n)=n,再根据MN=PQ=n,即可得出长方形MNQP的面积为n2.
解:由折叠可得,AF=AB=CD=GD=n,
∴FG=m﹣2n,AG=DF=m﹣n,
由折叠可得,DP=![]() DF=
DF=![]() (m﹣n),AM=
(m﹣n),AM=![]() AG=
AG=![]() (m﹣n),
(m﹣n),
∴MP=AD﹣AM﹣DP=m﹣2×![]() (m﹣n)=n,
(m﹣n)=n,
又∵MN=AB=n,
∴长方形MNQP的面积为n2,
故选:A.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
【题目】某人购进一批琼中绿橙到市场上零售,已知卖出的绿橙数量x(千克)与售价y(元)的关系如下表:
数量x(千克) | 1 | 2 | 3 | 4 | 5 | … |
售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 | … |
(1)写出售价y(元)与绿橙数量x(千克)之间的函数关系式;
(2)这个人若卖出50千克的绿橙,售价为多少元?