��Ŀ����
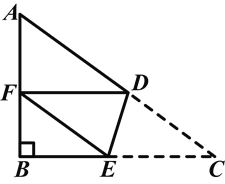
����Ŀ����ͼ����![]() �У�
�У�![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() .����
.����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ������
������![]() ���ٶ����
���ٶ����![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ������
������![]() ���ٶ����
���ٶ����![]() �˶����˶�ʱ����
�˶����˶�ʱ����![]() ��.
��.

��1���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���.
�ij���.
��2�����˶������У��Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() λ���߶�
λ���߶�![]() �Ĵ�ֱƽ�����ϣ������ڣ����
�Ĵ�ֱƽ�����ϣ������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��3���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
��4���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
���𰸡�(1)CP=8-3t;(2)������;(3)������;(4)������.
��������
��1��ֱ������![]() ������⣻
������⣻
��2�������߶δ�ֱƽ���ߵ����ʿɵ�![]() ���з�����⼴�ɣ�
���з�����⼴�ɣ�
��3������ȫ�������ε����ʿɵ���![]() ����Ϊ
����Ϊ![]() ��
��![]() ��
��
����ֻ��![]() ���з������
���з������![]() ��ֵ���ɣ�
��ֵ���ɣ�
��4����![]() ����Ϊ
����Ϊ![]() ������������
������������![]() ��
��![]() ����
����![]() ��
��![]() ��û�з���������t��ֵ���ʲ�����.
��û�з���������t��ֵ���ʲ�����.
�⣺��1��![]() ��
��
��2������![]() λ���߶�
λ���߶�![]() �Ĵ�ֱƽ�����ϣ�
�Ĵ�ֱƽ�����ϣ�
��![]() ��
��
��![]() ��
��
���![]() .
.
���Դ��ڣ�![]() ��ʱ��
��ʱ��![]() λ���߶�
λ���߶�![]() �Ĵ�ֱƽ������.
�Ĵ�ֱƽ������.
��3����![]() ��
��
��Ϊ![]() ��
��![]() ��
��
����ֻ��![]() ��
��
��![]() �����
�����![]() ��
��
���Դ���![]() .
.
��4����![]() ��
��
��Ϊ![]() ��
��
����������![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
����![]() ������.
������.
�ʴ�Ϊ��(1)CP=8-3t;(2)������;(3)������;(4)������.

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�