题目内容
【题目】已知,如图,ABCD中,BE,CF分别是∠ABC和∠BCD的角平分线,BE,CF相交于点O.
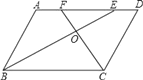
(1)求证:BE⊥CF;
(2)试判断AF与DE有何数量关系,并说明理由;
(3)当△BOC为等腰直角三角形时,四边形ABCD是何特殊四边形?(直接写出答案)
【答案】(1)见解析;(2)AF=DE,理由略;(3)四边形ABCD是矩形.
【解析】
(1)平行四边形中邻角互补,且BE、CF分别为一组邻角的平分线,所以BE和CF垂直.
(2)在三角形AEB中,因为BE为平分线,AD和BC平行,所以可得∠ABE=∠AEB,即AB=AE,同理,DF=DC,所以AF=DE.
(3)当△BOC为等腰直角三角形时,即∠BOC=90°,由题可知,∠ABC=∠BCD=90°,有一个角是直角的平行四边形为矩形.
(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD
∴∠ABC+∠BCD=180°
又∵BE,CF分别是∠ABC,∠BCD的平分线
∴∠EBC+∠FCB=90°
∴∠BOC=90°
故BE⊥CF;
(2)解:AF=DE
理由如下:
∵AD∥BC
∴∠AEB=∠CBE
又∵BE是∠ABC的平分线,
∴∠ABE=∠CBE
∴∠AEB=∠ABE
∴AB=AE
同理CD=DF
又∵四边形ABCD是平行四边形
∴AB=CD
∴AE=DF
∴AF=DE.

(3)解:当△BOC为等腰直角三角形时四边形ABCD是矩形.
理由:∵△BOC为等腰直角三角形,
∴∠BOC=90°,∠CBE=∠BCF=45°,
∵BE,CF分别是∠ABC和∠BCD的角平分线,
∴∠ABC=∠BCD=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.

练习册系列答案
相关题目