题目内容
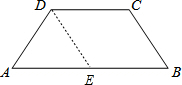
如图所示，在梯形ABCD中，AB∥CD，AD=BC=DC，且∠A=60°．
求证：AB=2CD．
求证：AB=2CD．
证明：作DE∥BC交AB于点E，
∵AB∥CD，
∴四边形DEBC是平行四边形，
∵AD=BC=DC，
∴BE=DC=AD=BC=DE
∵∠A=60°
∴△ADE是等边三角形
∴AE=EB=DC
∴AB=2DC
∵AB∥CD，
∴四边形DEBC是平行四边形，
∵AD=BC=DC，
∴BE=DC=AD=BC=DE
∵∠A=60°
∴△ADE是等边三角形
∴AE=EB=DC
∴AB=2DC
练习册系列答案
相关题目
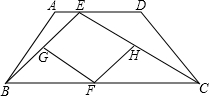别是BE、BC、CE的中点．
