题目内容
如图,在梯形ABCD中,AB∥CD,∠ABD=90°,AB=BD,在BC上截取BE,使BE=BA,过点B作BF⊥BC于B,交AD于点F.连接AE,交BD于点G,交BF于点H.
(1)已知AD=4
,CD=2,求sin∠BCD的值;
(2)求证:BH+CD=BC.

(1)已知AD=4
| 2 |
(2)求证:BH+CD=BC.

(1)在Rt△ABD中,∠ABD=90°,AB=BD,AD=4
,
则AB=BD=4,…(1分)
在Rt△CBD中,∠BDC=90°,CD=2,BD=4,
所以BC=
=2
,…(2分)
sin∠BCD=
=
=
.…(4分)
(2)证明:过点A作AB的垂线交BF的延长线于M.
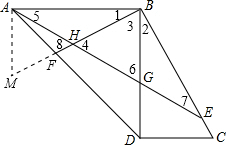
∵∠DBA=90°,∴∠1+∠3=90°.
∵BF⊥CB于B,∴∠3+∠2=90°.
∴∠2=∠1.…(5分)
∵BA=BD,∠BAM=∠BDC=90°,
∴△BAM≌△BDC.
∴BM=BC,AM=CD.…(7分)
∵EB=AB,∴∠7=∠5.
BH=BG.…(8分)
∴∠4=∠1+∠5=∠2+∠7=∠6.
∵∠8=∠4,∠MAH=∠6,
∴∠8=∠MAH,∴AM=MH=CD.…(9分)
∴BC=BM=BH+HM=BH+CD.…(10分)
其他解法,参照给分.
| 2 |
则AB=BD=4,…(1分)
在Rt△CBD中,∠BDC=90°,CD=2,BD=4,
所以BC=
| 22+42 |
| 5 |
sin∠BCD=
| BD |
| BC |
| 4 | ||
2
|
2
| ||
| 5 |
(2)证明:过点A作AB的垂线交BF的延长线于M.

∵∠DBA=90°,∴∠1+∠3=90°.
∵BF⊥CB于B,∴∠3+∠2=90°.
∴∠2=∠1.…(5分)
∵BA=BD,∠BAM=∠BDC=90°,
∴△BAM≌△BDC.
∴BM=BC,AM=CD.…(7分)
∵EB=AB,∴∠7=∠5.
BH=BG.…(8分)
∴∠4=∠1+∠5=∠2+∠7=∠6.
∵∠8=∠4,∠MAH=∠6,
∴∠8=∠MAH,∴AM=MH=CD.…(9分)
∴BC=BM=BH+HM=BH+CD.…(10分)
其他解法,参照给分.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目


 ∠ABD等于( )
∠ABD等于( )