题目内容
【题目】在平面直角坐标系 xOy 中,已知抛物线y= x2 -2px+q.
(1)当p=2 时,
①抛物线的顶点坐标横坐标为____ ___,纵坐标为__________(用含 q 的式子表示);
②若点 A(-1,y1),B(x2,y2 )都在抛物线上,且y2 >y1,令x2 = m,则 m的取值范围是_____________;
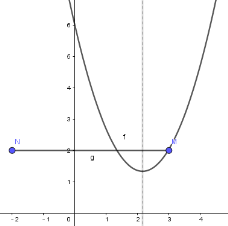
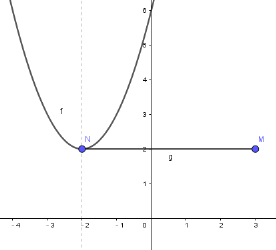
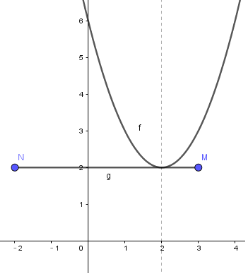
(2)已知点 M(3,2),将点 M 向左平移 5 个单位长度,得到点 N.当q=6 时,若抛物线与线段 MN 恰有一个公共点,结合函数图象,求 p 的取值范围为_____________.
【答案】(1)①2,q- 4;②m![]() 1或m
1或m ![]() 5;(2)p≤-2 或p=2或
5;(2)p≤-2 或p=2或![]() .
.
【解析】
(1)①将P的值代入,将函数解析式改写为顶点式,即可求解. ②由对称轴为x=2,可得x=-1与x=5的函数值相等,数形结合可知当y2 >y1时,x2的取值范围,即m的范围为x2 ![]() 1或x2
1或x2 ![]() 5
5
(2)由于线段MN//x轴,满足线段MN与抛物线只有一个交点,通过数形结合,分线段MN的左,右端点在抛物线上和抛物线的顶点在线段上三种情况,分别得到关于P的方程求解即可.
(1)①∵ p=2 ,
∴抛物线为y=x2 - 4x+q= (x- 2)2 +q- 4 .
∴顶点的坐标为( 2,q- 4).
②

由对称轴为x=2,由图可知,当x=-1与x=5的函数值相等,点A(-1,y1), B(x2,y2 ), 要使y2 >y1,则点B应在点A的左上方或在点![]() 的右上方,故有x2
的右上方,故有x2![]() 1或 x2
1或 x2![]() 5;而x2 = m,所以m的取值范围为m
5;而x2 = m,所以m的取值范围为m![]() 1或m
1或m ![]() 5.
5.
(2)∵点M(3,2)向左平移 5 个单位得到点N,
∴点N的坐标为(-2 ,2).
∵q= 6 ,
∴抛物线为y=x2 -2px+ 6 .
当抛物线经过点M(3,2)时, 2 = 32 - 6p+ 6 ,解得p![]() .
.
当抛物线经过点N(-2 ,2)时, 2 = (-2)2 + 4 p+ 6 ,解得 p=-2 .
当抛物线的顶点在线段PQ上时,6 - p2 = 2 ,解得p=±2 .
满足线段MN与抛物线只有一个交点,结合图象可知,m的取值范围是p≤-2 或p=2或![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案