题目内容
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( ) 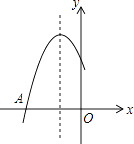
A.②④
B.①④
C.②③
D.①③
【答案】B
【解析】解:①∵图象与x轴有交点,对称轴为x= ![]() =﹣1,与y轴的交点在y轴的正半轴上, 又∵二次函数的图象是抛物线,
=﹣1,与y轴的交点在y轴的正半轴上, 又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2﹣4ac>0,
即b2>4ac,正确;
②∵抛物线的开口向下,
∴a<0,
∵与y轴的交点在y轴的正半轴上,
∴c>0,
∵对称轴为x= ![]() =﹣1,
=﹣1,
∴2a=b,
∴2a+b=4a,a≠0,
错误;
③∵x=﹣1时y有最大值,
由图象可知y≠0,错误;
④把x=1,x=﹣3代入解析式得a+b+c=0,9a﹣3b+c=0,两边相加整理得
5a﹣b=﹣c<0,即5a<b.
故选B.
由抛物线的开口向下知a<0,与y轴的交点在y轴的正半轴上得到c>0,由对称轴为x= ![]() =﹣1可以判定②错误;
=﹣1可以判定②错误;
由图象与x轴有交点,对称轴为x= ![]() =﹣1,与y轴的交点在y轴的正半轴上,可以推出b2﹣4ac>0,即b2>4ac,①正确;由x=﹣1时y有最大值,由图象可知y≠0,③错误.然后即可作出选择.
=﹣1,与y轴的交点在y轴的正半轴上,可以推出b2﹣4ac>0,即b2>4ac,①正确;由x=﹣1时y有最大值,由图象可知y≠0,③错误.然后即可作出选择.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
【题目】如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格:
点 | 坐标 | 所在象限或坐标轴 |
A | ||
B | ||
C | ||
D | ||
E | ||
F |

(2)在图上将回形图继续画下去(至少再画出4个拐点);
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系;