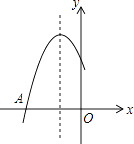题目内容
【题目】已知二次函数y=mx2﹣5mx+1(m为常数,m>0),设该函数的图象与y轴交于点A,该图象上的一点B与点A关于该函数图象的对称轴对称.
(1)求点A,B的坐标;
(2)点O为坐标原点,点M为该函数图象的对称轴上一动点,求当M运动到何处时,△MAO的周长最小.
【答案】
(1)解:当x=0时,y=1,则点A的坐标为(0,1),
∵抛物线对称轴为x= ![]() =
= ![]() ,
,
∴B点坐标为(5,1)
(2)解:设直线OB解析式为y=kx,把B(5,1)代入可得5k=1,解得k= ![]() ,
,
∴直线OB解析式为y= ![]() x,
x,
由轴对称的性质可知当点M运动到直线OB与二次函数对称轴的交点时,△MAO的周长最小.
当x= ![]() 时,y=
时,y= ![]() ,
,
∴M点的坐标为( ![]() ,
, ![]() )
)
【解析】(1)令x=0可求得y=1,可求得A点坐标,再利用对称性可求得B点坐标;(2)可先求得直线OB解析式,当点M运动到直线OB与二次函数对称轴的交点时,满足条件,可求得M点的坐标.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图: 某校60名学生体育测试成绩成绩统计表
成绩 | 划记 | 频数 | 频率 |
优秀 | 正正正 | a | 0.3 |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 0.15 |
不合格 |
| c | d |
合计 |
(说明:40﹣55分为不合格,55﹣70分为合格,70﹣85分为良好,85﹣100分为优秀)
请根据以上信息,解答下列问题:
(1)表中的a=;b=;c=;d= .
(2)请根据频数分布表,画出相应的频数分布直方图.
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.