Question

【题目】在△ABC 中，∠C=90°，AB 的中垂线交直线 BC 于 D，若∠BAD﹣∠DAC=22.5°，则∠B 的度数是_______

Answer 1

【答案】37.5°或 67.5°．

【解析】

求出AD=BD,推出∠B=∠DAB，∠B+∠BAC=90°， 分为两种情况并画出图形后，根据三角形内角和定理求出即可.

∵DE是AB的垂直平分线,

∴AD= BD,

∴∠B=∠DAB,

∵∠ACB= 90°，

∴∠B+∠BAC= 90°,

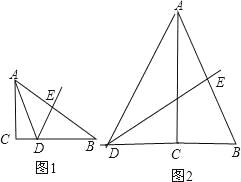
分为两种情况:①如图1,∵∠B+∠BAC= 90,∠BAD-∠DAC= 22.5°，

∴∠B=∠DAB=∠DAC+ 22.5°

∴∠DAC+ 22.5°+∠DAC+ 22.5° +∠DAC= 90°,∠DAC= 15°

∴∠B= 15°+ 22.5°= 37.5°

②如图2，∵∠B+∠BAC= 90° ,∠BAD-∠DAC= 22.5°

∴∠B=∠DAB=∠DAC+ 22.5°，

∴∠DAC+ 22.5° +∠DAC+ 22.5°- ∠DAC= 90° ，

∴∠DAC= 45° ,

∴∠B=45°+ 22.5°= 67.5°