��Ŀ����
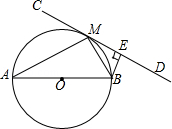
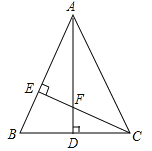
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
��1����ö��κ����Ľ���ʽ����M�����ꣻ
��2�������ö��κ���ͼ������ƽ��m��m��0������λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ������ڡ�ABC���ڲ�����������ABC�ı߽磩����m��ȡֵ��Χ��
��3����P��ֱ��AC�ϵĶ��㣬����P����C����M�����ɵ����������BCD���ƣ���ֱ��д�����е�P�����ֱ꣨��д�����������д�����̣���
���𰸡�
��1��
�⣺�ѵ�A��3��1������C��0��4��������κ���y=��x2+bx+c�ã�
![]() ���
��� ![]()
����κ�������ʽΪy=��x2+2x+4��
�䷽��y=����x��1��2+5��
���M��������1��5��
��2��
�⣺��ֱ��AC����ʽΪy=kx+b���ѵ�A��3��1����C��0��4������ã�
![]() ���
��� ![]()
��ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1���ABC���߷ֱ��ڵ�E����F
��x=1����ֱ��AC����ʽy=��x+4���y=3�����E����Ϊ��1��3������F����Ϊ��1��1��
��1��5��m��3�����2��m��4

��3��
�⣺����MC����MG��y�Ტ�ӳ���AC�ڵ�N�����G����Ϊ��0��5��
��MG=1��GC=5��4=1
��MC= ![]() =
= ![]() ��
��
��y=5����y=��x+4���x=��1�����N��������1��5����
��NG=GC��GM=GC��
���NCG=��GCM=45�㣬
���NCM=90�㣬
�ɴ˿�֪������P��AC�ϣ����MCP=90�㣬���D���C��Ϊ���������ζ�Ӧ��
�����С�PCM�ס�BDC������ ![]()
��BD=1��CD=3��
��CP= ![]() =
= ![]() =
= ![]() ��
��
��CD=DA=3��
���DCA=45�㣬
����P��y���Ҳ࣬��PH��y�ᣬ
�ߡ�PCH=45�㣬CP= ![]()
��PH= ![]() =
= ![]()
��x= ![]() ����y=��x+4�����y=
����y=��x+4�����y= ![]() ��
��
��P1�� ![]() ����
����
ͬ���ɵã�����P��y����࣬���x=�� ![]() ����y=��x+4�����y=
����y=��x+4�����y= ![]()
��P2�� ![]() ����
����
�����С�PCM�ס�CDB������ ![]()
��CP= ![]() =3
=3 ![]()
��PH=3 ![]() ��
�� ![]() =3��
=3��
����P��y���Ҳ࣬��x=3����y=��x+4�����y=1��
����P��y����࣬��x=��3����y=��x+4�����y=7
��P3��3��1����P4����3��7����
�����з�������õ�P������4�����ֱ�ΪP1�� ![]() ����P2��
����P2�� ![]() ����P3��3��1����P4����3��7��
����P3��3��1����P4����3��7��

����������1������A����C��������뺯������ʽ���������b��c��ֵ��ͨ���䷽���õ���M�����ꣻ��2����M�����ŶԳ���ֱ��x=1����ƽ�Ƶģ��������ֱ��AC�Ľ���ʽ����x=1���������M������ƽ��ʱ��AC��AB�ཻʱy��ֵ�����ɵõ�m��ȡֵ��Χ����3������������ɵá�MCP=90�㣬������PCM���BCD���ƣ���Ҫ���з������ۣ��ֳɡ�PCM�ס�BDC���PCM�ס�CDB���֣�Ȼ�����ñߵĶ�Ӧ��ֵ��������꣮

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�