ΧβΡΩΡΎ»ί
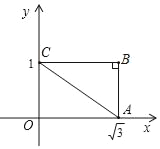
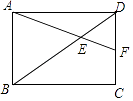
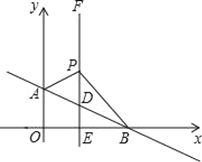
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏABΘΚy=©¹![]() x+bΫΜy÷α”ΎAΘ®0Θ§1Θ©Θ§ΫΜx÷α”ΎΒψBΘ°ΙΐΒψEΘ®1Θ§0Θ©Ήςx÷αΒΡ¥ΙœΏEFΫΜAB”ΎΒψDΘ§P «÷±œΏEF…œ“ΜΕ·ΒψΘ§«“‘ΎΒψDΒΡ…œΖΫΘ§…ηPΘ®1Θ§nΘ©Θ°
x+bΫΜy÷α”ΎAΘ®0Θ§1Θ©Θ§ΫΜx÷α”ΎΒψBΘ°ΙΐΒψEΘ®1Θ§0Θ©Ήςx÷αΒΡ¥ΙœΏEFΫΜAB”ΎΒψDΘ§P «÷±œΏEF…œ“ΜΕ·ΒψΘ§«“‘ΎΒψDΒΡ…œΖΫΘ§…ηPΘ®1Θ§nΘ©Θ°
Θ®1Θ©÷±œΏABΒΡ±μ¥ο ΫΈΣ__________________ΘΜ
Θ®2Θ©ΔΌ«σΓςABPΒΡΟφΜΐΘ®”ΟΚ§nΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
ΔΎΒ±SΓςABP=2 ±Θ§«σΒψPΒΡΉχ±ξΘΜ
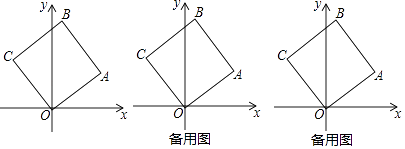
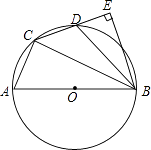
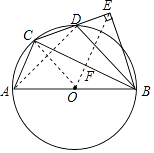
Δέ‘ΎΔΎΒΡΧθΦΰœ¬Θ§“‘PBΈΣ±Ώ‘ΎΒΎ“ΜœσœόΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈBPCΘ§«κ÷±Ϋ”–¥≥ωΒψCΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩ(1)y=©¹![]() x+1ΘΜ(2)ΔΌSΓςABP=
x+1ΘΜ(2)ΔΌSΓςABP=![]() ΘΜΔΎPΘ®1Θ§2Θ©ΘΜΔέΘ®3Θ§4Θ©ΜρΘ®5Θ§2Θ©ΜρΘ®3Θ§2Θ©Θ°
ΘΜΔΎPΘ®1Θ§2Θ©ΘΜΔέΘ®3Θ§4Θ©ΜρΘ®5Θ§2Θ©ΜρΘ®3Θ§2Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Α―AΒΡΉχ±ξ¥ζ»κ÷±œΏABΒΡΫβΈω ΫΦ¥Ω…«σΒΟbΒΡ÷ΒΘ§”…¥ΥΦ¥Ω…«σΒΟ÷±œΏABΒΡΫβΈω ΫΘΜΘ®2Θ©ΔΌΙΐΒψAΉςAMΓΆPDΘ§¥ΙΉψΈΣMΘ§«σΒΟAMΒΡ≥ΛΘ§‘Ό«σΒΟΓςBPDΚΆΓςPABΒΡΟφΜΐΘ§Εΰ’ΏΒΡΚΆΦ¥ΈΣΓςABPΒΡΟφΜΐΘΜΔΎΒ±SΓςABP=2 ±Θ§¥ζ»κΔΌ÷–ΥυΒΟΒΡ¥ζ ΐ ΫΘ§«σΒΟn÷ΒΘ§Φ¥Ω…«σΒΟΒψPΒΡΉχ±ξΘΜΔέΖ÷P «÷±Ϋ«ΕΞΒψ«“BP=PCΓΔB «÷±Ϋ«ΕΞΒψ«“BP=BC ΓΔC «÷±Ϋ«ΕΞΒψ«“CP=CB»ΐ÷÷«ιΩω«σΒψCΒΡΉχ±ξΦ¥Ω…Θ°
Θ®1Θ©ΓΏy=-![]() x+bΨ≠ΙΐAΘ®0Θ§1Θ©Θ§
x+bΨ≠ΙΐAΘ®0Θ§1Θ©Θ§
Γύb=1Θ§
Γύ÷±œΏABΒΡΫβΈω Ϋ «y=-![]() x+1ΘΜ
x+1ΘΜ
Ι ¥πΑΗΈΣΘΚy=-![]() x+1ΘΜ
x+1ΘΜ
Θ®2Θ©ΔΌΙΐΒψAΉςAMΓΆPDΘ§¥ΙΉψΈΣMΘ§‘ρ”–AM=1Θ§
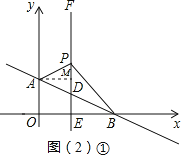
ΓΏx=1 ±Θ§y=-![]() x+1=
x+1=![]() Θ§P‘ΎΒψDΒΡ…œΖΫΘ§
Θ§P‘ΎΒψDΒΡ…œΖΫΘ§
ΓύPD=n-![]() Θ§SΓςAPD=
Θ§SΓςAPD=![]() PDAM=
PDAM=![]() ΓΝ1ΓΝΘ®n
ΓΝ1ΓΝΘ®n![]() Θ©=
Θ©=![]() n
n![]() Θ§
Θ§
”…ΒψBΘ®3Θ§0Θ©Θ§Ω…÷ΣΒψBΒΫ÷±œΏx=1ΒΡΨύάκΈΣ2Θ§Φ¥ΓςBDPΒΡ±ΏPD…œΒΡΗΏ≥ΛΈΣ2Θ§
ΓύSΓςBPD=![]() PDΓΝ2=n-
PDΓΝ2=n-![]() Θ§
Θ§
ΓύSΓςPAB=SΓςAPD+SΓςBPD=![]() n-
n-![]() +n-
+n-![]() =
=![]() n-1ΘΜ
n-1ΘΜ
ΔΎΒ±SΓςABP=2 ±Θ§![]() n-1=2Θ§
n-1=2Θ§
ΫβΒΟn=2Θ§
ΓύΒψPΘ®1Θ§2Θ©Θ°
ΔέΓΏEΘ®1Θ§0Θ©Θ§
ΓύPE=BE=2Θ§
ΓύΓœEPB=ΓœEBP=45ΓψΘ°
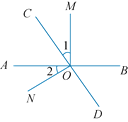
ΒΎ1÷÷«ιΩωΘ§»γΆΦ1Θ§ΓœCPB=90ΓψΘ§BP=PCΘ§
ΙΐΒψCΉςCNΓΆ÷±œΏx=1”ΎΒψNΘ°
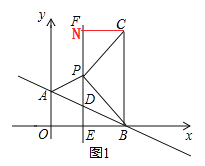
ΓΏΓœCPB=90ΓψΘ§ΓœEPB=45ΓψΘ§
ΓύΓœNPC=ΓœEPB=45ΓψΘ§
‘ΎΓςCNP”κΓςBEP÷–Θ§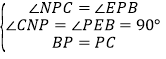 Θ§
Θ§
ΓύΓςCNPΓ’ΓςBEPΘ§
ΓύPN=NC=EB=PE=2Θ§
ΓύNE=NP+PE=2+2=4Θ§
ΓύCΘ®3Θ§4Θ©Θ°
ΒΎ2÷÷«ιΩωΘ§»γΆΦ2Θ§ΓœPBC=90ΓψΘ§BP=BCΘ§
ΙΐΒψCΉςCFΓΆx÷α”ΎΒψFΘ°
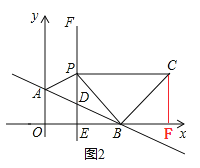
ΓΏΓœPBC=90ΓψΘ§ΓœEBP=45ΓψΘ§
ΓύΓœCBF=ΓœPBE=45ΓψΘ§
‘ΎΓςCBP”κΓςPBE÷–Θ§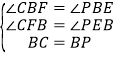 Θ§
Θ§
ΓύΓςCBFΓ’ΓςPBEΘ°
ΓύBF=CF=PE=EB=2Θ§
ΓύOF=OB+BF=3+2=5Θ§
ΓύCΘ®5Θ§2Θ©Θ°
ΒΎ3÷÷«ιΩωΘ§»γΆΦ3Θ§ΓœPCB=90ΓψΘ§CP=CBΘ§
ΓύΓœCPB=ΓœCBP=45ΓψΘ§
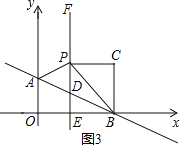
ΓΏΓœEPB=ΓœEBP=45ΓψΘ§
ΓύΓœPCB=ΓœCBE=ΓœEPC=90ΓψΘ§
ΓύΥΡ±Ώ–ΈEBCPΈΣΨΊ–ΈΘ§
ÿCP=CBȧ
ΓύΥΡ±Ώ–ΈEBCPΈΣ’ΐΖΫ–ΈΘ§
ΓύPC=CB=PE=EB=2Θ§
ΓύCΘ®3Θ§2Θ©Θ°
Γύ“‘PBΈΣ±Ώ‘ΎΒΎ“ΜœσœόΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈBPCΘ§ΒψCΒΡΉχ±ξ «Θ®3Θ§4Θ©ΜρΘ®5Θ§2Θ©ΜρΘ®3Θ§2Θ©Θ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ