Question

【题目】已知线段AB=(为常数)，点C为直线AB上一点，点P、Q分别在线段BC、AC上，且满足CQ=2AQ，CP=2BP.

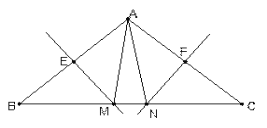
(1)如图，当点C恰好在线段AB中点时，则PQ=_______(用含的代数式表示)；

(2)若点C为直线AB上任一点，则PQ长度是否为常数?若是，请求出这个常数；若不是，请说明理由；

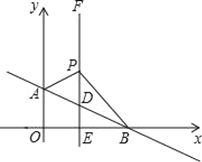
(3)若点C在点A左侧，同时点P在线段AB上(不与端点重合)，请判断2AP+CQ-2PQ与1的大小关系，并说明理由。

Answer 1

【答案】（1）；（2）；（3）2AP+CQ-2PQ＜1

【解析】

（1）设AQ=x，BP=y，则CQ=2x，CP=2y．由AB=AQ+CQ+CP+PB= m，得到x+y=，由PQ=QC+CP=2x+2y即可得到结论；

（2）分五种情况讨论：①若C在线段AB上；②若C在A的左边；③若C在B的右边；④若B与C重合，⑤若A与C重合．

（3）设AQ=x，BP=y，则CQ=2x，CP=2y．根据（2）得到PQ=，AP=PQ－AQ=．

代入2AP+CQ-2PQ即可得到结论．

（1）设AQ=x，BP=y，则CQ=2x，CP=2y．

∵AB=AQ+CQ+CP+PB= m，∴x+2x+2y+y=m，∴x+y=，PQ=QC+CP=2x+2y=2(x+y)=．

（2）分五种情况讨论：

①若C在线段AB上，由（1）可得：PQ=．

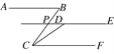
②若C在A的左边，如图1．

设AQ=x，BP=y，则CQ=2x，CP=2y．

∵AB=CB－CA= (CP+PB)－（CQ+AQ）=m，∴（2y+y）－（x+2x）=m，∴y－x=，PQ=CP－CQ=2y－2x=2(y－x)=．

③若C在B的右边，如图2．

设AQ=x，BP=y，则CQ=2x，CP=2y．

∵AB=CA－CB= （CQ+AQ）－(CP+PB) =m，∴（2x+x）－（2y+y）=m，∴x－y=，PQ= CQ －CP=2x－2y=2(x－y)=．

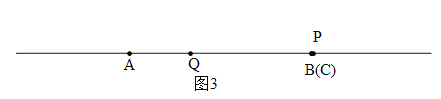
④若B与C重合，则P与B也重合，如图3．

设AQ=x，则CQ=BQ=2x，CP=2BP=0，∴PQ=BQ=2x，AB=3x=m，∴PQ=．

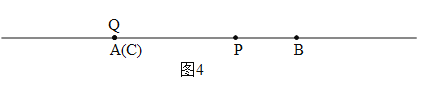
⑤若A与C重合，则Q与A也重合，如图4．

设BP=y，则CQ=AQ=0，CP=2BP=2y，∴PQ=CP=2y，AB=3y=m，∴PQ=．

综上所述：点C为直线AB上任一点，则PQ长度为常数．

（3）如图1．设AQ=x，BP=y，则CQ=2x，CP=2y．PQ=CP－CQ=2y－2x=2(y－x)=．

AP=PQ－AQ=．2AP+CQ-2PQ==0，∴2AP+CQ-2PQ＜1．