题目内容
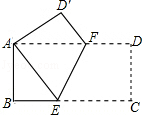
【题目】如图,矩形ABCD中,AB= ![]() ,BC=
,BC= ![]() ,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则
,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则 ![]() 等于( )
等于( ) 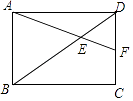
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:∵四边形ABCD是矩形, ∴∠BAD=90°,又AB= ![]() ,BC=
,BC= ![]() ,
,
∴BD= ![]() =3,
=3,
∵BE=1.8,
∴DE=3﹣1.8=1.2,
∵AB∥CD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,DF= ![]() ,
,
则CF=CD﹣DF= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
故选A.
【考点精析】掌握矩形的性质和相似三角形的判定与性质是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目