题目内容
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E. 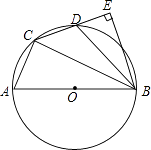
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB= ![]() ,求OE的长度.
,求OE的长度. 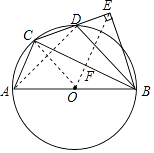
【答案】
(1)解:连接AD,

∵D为弧AB的中点,
∴AD=BD,
∵AB为直径,
∴∠ADB=90°,
∴∠DAB=∠DBA=45°,
∴∠DCB=∠DAB=45°
(2)解:证明:∵BE⊥CD,又∵∠ECB=45°,
∴∠CBE=45°,
∴CE=BE,
∵四边形ACDB是圆O的内接四边形,
∴∠A+∠BDC=180°,
又∵∠BDE+∠BDC=180°,
∴∠A=∠BD,
又∵∠ACB=∠BED=90°,
∴△ABC∽△DBE,
∴DE:AC=BE:BC,
∴DE:BE=AC:BC=1:2,
又∵CE=BE,
∴DE:CE=1:2,
∴D为CE的中点
(3)解:∵CO=BO,CE=BE,
∴OE垂直平分BC,
∴F为BC中点,
又∵O为AB中点,
∴OF为△ABC的中位线,
∴OF= ![]() AC,
AC,
∵∠BEC=90°,EF为中线,
∴EF= ![]() BC,
BC,
在Rt△ACB中,AC2+BC2=AB2,
∵AC:BC=1:2,AB= ![]() ,
,
∴AC= ![]() ,BC=2
,BC=2 ![]() ,
,
∴OE=OF+EF=1.5 ![]() .
.
【解析】(1)连接AD,由D为弧AB的中点,得到AD=BD,根据圆周角定理即可得到结论;(2)由已知条件得到∠CBE=45°,根据圆内接四边形的性质得到∠A=∠BD,根据相似三角形的性质得到DE:AC=BE:BC,即可得到结论.(3)连接CO,根据线段垂直平分线的判定定理得到OE垂直平分BC,由三角形的中位线到现在得到OF= ![]() AC,根据直角三角形的性质得到EF=
AC,根据直角三角形的性质得到EF= ![]() BC,由勾股定理即可得到结论.
BC,由勾股定理即可得到结论.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?