题目内容
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() 垂直平分
垂直平分![]() .
.

【答案】(1)见详解;(2)见详解
【解析】
(1)根据ASA判定△ACD≌△CBF即可;
(2)由(1)得到BF=CD,由D为BC中点,根据中点定义得到CD=BD,等量代换得到BF=BD,再根据角度之间的数量关系求出∠ABC=∠ABF,即BA是∠FBD的平分线,从而利用等腰三角形三线合一的性质求证即可.
解:(1)∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
∵AC=CB,
∴△ACD≌△CBF;
(2)连接DF,
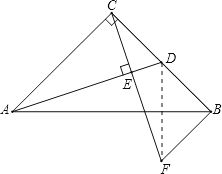
由(1)得CD=BF
∵![]() 为
为![]() 边上的中点
边上的中点
∴CD=BD=![]() BC
BC
∴BF=BD
∴△BFD为等腰直角三角形
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴根据等腰三角形三线合一的性质有BA⊥FD,BA平分边FD,
即AB垂直平分DF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图,是我国第24~30届奥运奖牌数的回眸和中国代表团奖牌总数统计图,根据表和统计图,以下描述正确的是( )
金牌(块) | 银牌(块) | 铜牌(块) | 总计奖牌数 | |
24 | 5 | 11 | 12 | 28 |
25 | 16 | 22 | 12 | 54 |
26 | 16 | 22 | 12 | 50 |
27 | 28 | 16 | 15 | 59 |
28 | 32 | 17 | 14 | 63 |
29 | 51 | 21 | 28 | 100 |
30 | 38 | 27 | 23 | 88 |

A.中国代表团的奥运奖牌总数一直保持上升趋势
B.折线统计图中的六条线段只是为了便于观察图象所反映的变化,不表示某种意思
C.与第29届北京奥运会相比,奥运金牌数、银牌数、铜牌数都有所下降
D.评价一个代表团在一届奥运会上的表现,我们只需关注金牌数,无需考虑其他