题目内容
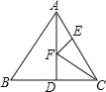
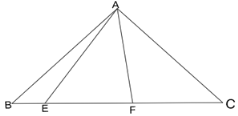
【题目】已知:如图,等腰直角三角形ABC中,∠BAC=90°,BA=AC,点E、F是线段BC上两动点且∠EAF=45°,请写出BE、EF、FC之间的等量关系并证明.
【答案】BE2+ FC2= EF2,证明见解析.
【解析】
将△ABE逆时针旋转90度到△ACD的位置,点B、E的对应点为点C、D,首先证明∠EAF=∠FAD=45°,然后利用SAS证明△AEF≌△ADF,得到EF=DF,求出∠FCD=90°,根据勾股定理可得结论.
BE2+ FC2= EF2,
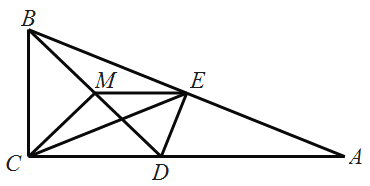
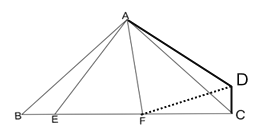
证明:如图,将△ABE逆时针旋转90度到△ACD的位置,点B、E的对应点为点C、D,
∴AE=AD,∠BAE=∠CAD,BE=CD,
∵∠EAF=45°,
∴∠BAE+∠FAC=45°,
∴∠CAD +∠FAC=45°,
∴∠EAF=∠FAD=45°,
又∵AE=AD,AF=AF,
∴△AEF≌△ADF(SAS),
∴EF=DF,
∵∠ACD=∠ABE=∠ACB=45°,
∴∠FCD=90°,
∴FC2+CD2=DF2,即BE2+ FC2= EF2.

练习册系列答案
相关题目