题目内容
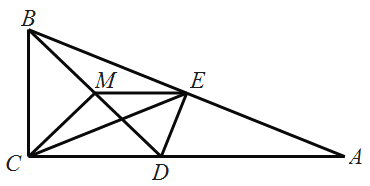
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片,使AD落在BC上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB,AC于点E、G,连结GF,给出下列结论①∠AGD=110.5°;②S△AGD=S△OGD;③四边形AEFG是菱形;④BF=![]() OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8
OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8![]() ,其中正确的有( )个.
,其中正确的有( )个.
A.2个B.3个C.4个D.5个
【答案】B
【解析】
①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数,从而求得∠AGD;
②证△AEG≌△FEG得AG=FG,由FG>OG即可得;
③先计算∠AGE=∠GAD+∠ADG=67.5°,∠AED=∠AGD-∠EAG=67.5°,从而得到∠AGE=∠AED,易得AE=AG,由AE=FE、AG=FG即可得证;
④设OF=a,先求得∠EFG=45°,易得∠GFO=45°,在Rt△OFG中,GF=![]() OF=
OF=![]() a,从而可证得BF=EF=GF=
a,从而可证得BF=EF=GF=![]() OF;
OF;
⑤由S△OGF=1求出a2,再表示出BE及AE的长,利用正方形的面积公式可得出结论.
解:∵四边形ABCD是正方形,
∴∠EAG=∠GAD=∠ADO=45°,∠AOB=90°,
由折叠的性质可得:∠ADG=![]() ∠ADO=22.5°,
∠ADO=22.5°,
∴∠AGD=180°-∠GAD-∠ADG=112.5°,
故①错误;
由折叠的性质可得:AE=EF,∠AEG=∠FEG,
在△AEG和△FEG中,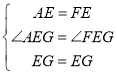 ,
,
∴△AEG≌△FEG(SAS),
∴AG=FG,
∵在Rt△GOF中,AG=FG>GO,
∴S△AGD>S△OGD,故②错误;
∵∠AGE=∠GAD+∠ADG=67.5°,∠AED=∠AGD-∠EAG=67.5°,
∴∠AGE=∠AED,
∴AE=AG,
又∵AE=FE,AG=FG,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,故③正确;
设OF=a,
∵△AEG≌△FEG,
∴∠EFG=∠EAG=45°,
又∵∠EFO=90°,
∴∠GFO=45°,
∴在Rt△OFG中,GF=![]() OF=
OF=![]() a,
a,
∵∠EFO=90°,∠EBF=45°,
∴在Rt△EBF中,BF=EF=GF=![]() a,即BF=
a,即BF=![]() OF,故④正确;
OF,故④正确;
∵S△OGF=1,
∴![]() OF2=1,即
OF2=1,即![]() a2=1,
a2=1,
则a2=2,
∵BF=EF=![]() a,且∠BFE=90°,
a,且∠BFE=90°,
∴BE=2a,
又∵AE=EF=![]() a,
a,
∴AB=AE+BE=![]() a+2a=(2+
a+2a=(2+![]() )a,
)a,
则正方形ABCD的面积是(2+![]() )2a2=(6+
)2a2=(6+![]() )×2=12+
)×2=12+![]() ,
,
故⑤正确;
故选:B.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案