Question

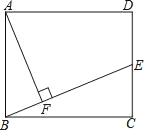
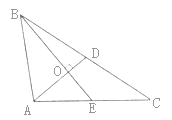
【题目】如图，在△ABC中，AC=3，BC=4，若AC，BC边上的中线BE,AD垂直相交于点O，则AB=________.

Answer 1

【答案】

【解析】

利用三角形中线定义得到BD=2，AE=，且可判定点O为△ABC的重心，所以AO=2OD，OB=2OE，利用勾股定理得到BO2+OD2=4，OE2+AO2=，等量代换得到BO2+ AO2=4，BO2+AO2=，把两式相加得到BO2+AO2=5，然后再利用勾股定理可计算出AB的长．

解：∵AD、BE为AC，BC边上的中线，
∴BD=BC=2，AE=AC=，点O为△ABC的重心，
∴AO=2OD，OB=2OE，
∵BE⊥AD，
∴BO2+OD2=BD2=4，OE2+AO2=AE2=，
∴BO2+AO2=4，BO2+AO2=，
∴BO2+AO2= ，
∴BO2+AO2=5，
∴AB==．
故答案为．